概述
CELF(Cost Effective Lazy Forward,具有成本效益的惰性前向选择)算法可以在一个有传播行为的网络中选取一些种子节点作为传播源头,以达到影响力最大化(Influence Maximumization, IM)的效果。CELF 算法由 Jure Leskovec 等人于 2007 年提出,它改进了传统基于 IC 模型的贪心算法,利用函数次模性,只在初始时计算所有节点的影响力,之后不再重复计算所有节点的影响力,因此具有更高的成本效益。CELF 算法的一个典型应用场景是预防流行病爆发,通过选择出一小组人进行监测,从而达到任何疾病在爆发的早期就能被发现的效果。
算法的相关资料如下:
- J Leskovec, A. Krause, C. Guestrin, C. Faloutsos, J. VanBriesen, N. Glance, Cost-effective Outbreak Detection in Networks (2007)
- D. Kempe, J. Kleinberg, E. Tardos, Maximizing the Spread of Influence through a Social Network (2003)
基本概念
IC 模型
在研究一个系统时,常用的方法是将系统抽象为数学模型,通过研究数学模型来研究系统,这个过程称为仿真或模拟。对于影响力最大化问题,最常用的模型之一就是 IC 模型。
IC 模型,即独立级联模型(Independent Cascade Model),是一种概率型传播模型,它的基本框架如下:
- 初始时,图中所有节点未激活,选定一个种子集合,激活该集合内的节点。
- 首轮传播中,种子节点以一定的概率尝试激活尚未被激活的出边邻居节点,不论是否成功,都只进行一次尝试。
- 下一轮传播中,只有在上一轮新被激活的节点具备激活能力,同样地,它们会以一定的概率尝试激活尚未被激活的出边邻居节点,不论是否成功,都只进行一次尝试。
- 当图中剩余具备激活能力的节点数为 0 时,传播过程结束。
传播结束时,图中被激活的节点总量就可以衡量种子集合的影响力。Ultipa 的 CELF 算法采用 IC 模型模拟传播过程:给定一个激活(传播)概率 p,具备激活能力节点每次进行激活尝试时,系统均匀随机抽取一个 0~1 范围内的数字 random,如果 random < p,则激活成功。
很显然,IC 模型的模拟结果受概率影响,有随机性。因此,我们采用蒙特卡罗模拟(Monte-Carlo Simulation),简单来说就是通过大量次数的模拟,对结果取平均值,从而得到一个近似的确定值。
次模性
次模性(Submodular,又称子模性)是集合函数的一个属性,它描述的是一种边际效益(Marginal Gain)递减的现象。对于集合函数 f(),有集合 A ⊆ B ⊆ V 和元素 e ∈ V-B,满足以下条件则说明函数有次模性:

这意味着,在函数的f() 的作用下,随着集合内元素的增多,元素 e 的边际效益递减。
计算种子集合影响力的函数 IC() 具有次模性,CELF 算法正是利用了 IC() 函数的次模性对传统的贪心算法进行了改进,省去了大量的重复计算,效率较贪心算法提升了约 700 倍,但结果基本保持一致。
次模函数最大化
影响力最大化问题可以看做是次模函数最大化问题,具有以下形式:
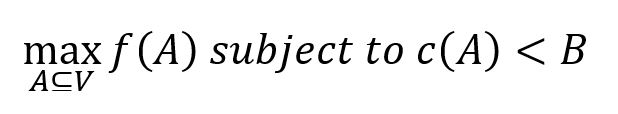
其中,函数 f() 有次模性,A 是输入集合,c(A) 是针对 A 的一个约束条件,要求满足 c(A) 小于条件 B。本算法的约束条件是简单的基数约束,即 c(A) = |A| < k,要求选取不超过 k 个元素的子集使得函数结果尽可能大。
次模函数最大化是 NP 难问题,只能求近似最优解。
特殊处理
孤点、不连通图
孤点不与任何其它节点相连,其影响力为 0。
对于不连通图,节点的影响力在各连通分量内进行传播。
自环边
节点不能通过自环边激活其他节点,因此节点的自环边不影响节点的影响力。
有向边
节点的影响力与其出边的数量有关。
命令及配置项
- 命令:
algo(celf) params()参数配置项如下:
| 名称 | 类型 |
默认值 |
规范 |
描述 |
|---|---|---|---|---|
| seedSetSize | int | 1 | >=1 | 种子节点个数 |
| monteCarloSimulations | int | 1000 | >=1 | 蒙特卡罗模拟次数 |
| propagationProbability | float | 0.1 | (0,1) | 节点被激活的概率 |
示例:在图上运行 CELF 算法,节点被激活状态邻居激活的概率为 0.5,蒙特卡洛模拟 1000 次,找出 3 个种子节点
algo(celf).params({
seedSetSize: 3,
monteCarloSimulations: 1000,
propagationProbability: 0.5 }) as seeds
return seeds
算法执行
任务回写
1. 文件回写
| 配置项 | 各列数据 |
|---|---|
| filename | _id,spread |
示例:在图上运行 CELF 算法,节点被激活状态邻居激活的概率为 0.5,蒙特卡洛模拟 1000 次,找出 3 个种子节点,将算法结果回写至名为 seeds 的文件
algo(celf).params({
seedSetSize: 3,
monteCarloSimulations: 1000,
propagationProbability: 0.5
}).write({
file:{
filename: "seeds"}})
2. 属性回写
算法不支持属性回写。
3. 统计回写
算法无统计值。
直接返回
| 别名序号 | 类型 | 描述 | 列名 |
|---|---|---|---|
| 0 | []perNode | 点及其边际效益 | _uuid, spread |
示例:在图上运行 CELF 算法,节点被激活状态邻居激活的概率为 0.5,蒙特卡洛模拟 1000 次,找出 3 个种子节点,将算法结果定义为别名 seeds 并返回
algo(celf).params({
seedSetSize: 3,
monteCarloSimulations: 1000,
propagationProbability: 0.5 }) as seeds
return seeds
流式返回
| 别名序号 | 类型 | 描述 | 列名 |
|---|---|---|---|
| 0 | []perNode | 点及其边际效益 | _uuid, spread |
示例:在图上运行 CELF 算法,节点被激活状态邻居激活的概率为 0.5,蒙特卡洛模拟 1000 次,找出 3 个种子节点,返回种子节点的 ID、createdTime 属性信息和边际效益
algo(celf).params({
seedSetSize: 3,
monteCarloSimulations: 1000,
propagationProbability: 0.5 }).stream() as seeds
find().nodes({_uuid == seeds._uuid}) as nodes
return table(nodes._id, nodes.createdTime, seeds.spread)
实时统计
算法无统计值。
