概述
HANP(Hop Attenuation & Node Preference,跳跃衰减和节点倾向性)算法是对标签传播算法(LPA)的扩展,它在 LPA 的基础上引入了标签分值衰减机制,并考虑了邻居节点的度对邻居标签权重的影响。该算法由 Ian X.Y. Leung 于 2009 年提出。
算法的相关资料如下:
- I.X.Y. Leung, P. Hui, P. Liò, J. Crowcroft, Towards real-time community detection in large networks (2009)
基本概念
标签分值
标签分值代表标签的传播能力。HANP 算法给每个标签赋予的初始分值为 1,当节点从邻居节点选取新标签时(即标签跳跃一次),新标签传递到节点上的分值会有一定程度的衰减,这正是算法名称中 HA(Hop Attenuation,跳跃衰减)的来源。标签分值每次跳跃后衰减的幅度称为衰减因子,记作 δ,衰减因子能有效地避免大社区的形成。下图中,令 δ = 0.3,当绿色节点选取标签 a 时,标签 a 在绿色节点上的分值衰减为 2 - 0.3 = 1.7。
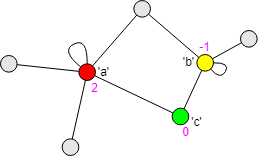
当选取的新标签来自多个邻居时,选取分值最高的进行衰减。
节点度倾向性
节点度倾向性指的是度越大的节点传播标签的能力越强;换句话说,一个节点会倾向于接受节点度较高的邻居的标签。HANP 算法名称中 NP 的全称 Node Preference(节点倾向性)指的就是这种对邻居节点的度的倾向性。
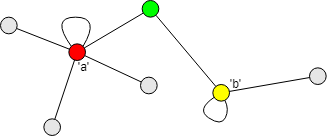
如上图所示,作为绿色节点的邻居,红色节点的度为 6(自环边计算两次),黄色节点的度为 4,因此绿色节点更倾向于接受标签 a。
当然,也可以规定度较低的节点标签得到优先传播。因此,算法考虑标签所在节点的度的指数幂,当指数大于 0 时,节点度高的标签会得到优先传播;当指数小于 0 时,节点度低的标签会得到优先传播;当指数等于 0 时,节点度不影响标签传播的优先级。
标签权重
节点 j 的标签 l 向其邻居节点 i 传播时的权重 w(l) 等于标签 l 在 j 上的分值 s(j)、j 的度的幂函数、i 和 j 之间的边权重和这三者的乘积;当 i 有多个邻居节点拥有标签 l 时,需要对来自所有邻居节点的标签 l 权重求和:
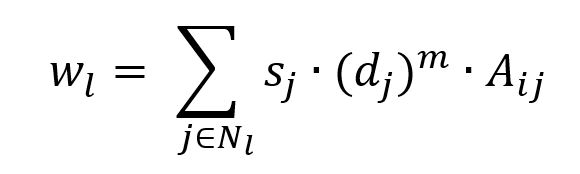
上式中,d(j) 为 j 的节点度,m 为幂指数,A(ij) 为 i、j 之间的边权重和。
对于图中任意节点 i,l 为 i 的邻居的标签,w(l) 为 l 的权重,则 i 的新标签 l' 可表示为:
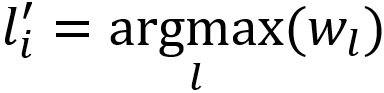
令 s(l') 为新标签在原各个邻居节点上的分值,δ 为衰减因子,则新标签在 i 上的分值为:
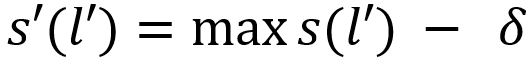
请注意,如果选取的新标签与节点当前的标签相同,则 δ = 0,即不进行分值衰减。
HANP 算法的迭代过程与 LPA 类似。在算法开始时将所有点的标签分值设置为 1;在每轮迭代中,为每个节点计算是否能从其邻居节点中选取与现有标签不同标签,或比现有标签分值更高的相同标签;计算完所有节点后,对需要更新的节点进行更新。按此规则循环迭代至所有节点的标签和标签分值不再变化,或迭代轮数达到限制。
与 LPA 不同的是,由于 HANP 算法引入了标签分值,杜绝了标签震荡的情况,因此不需要额外的中断机制。
特殊处理
孤点、不连通图
对于不连通图,各孤点、连通分量之间没有邻边,不能相互传递标签,不含有相同初始标签的连通分量不会被划分为相同社区。
自环边
HANP 算法对自环边的处理与节点度算法 algo(degree) 相同,都是将每条自环边计算两次。
有向边
对于有向边,HANP 算法会忽略边的方向,按照无向边进行计算。
结果和统计值
以下面的图为例,边的权重均为 1,节点内的字母是初始标签,节点 11 没有初始标签,运行 HANP 算法,迭代 10 次,幂指数 m 为 0.1,衰减因子 δ 为 0.2:
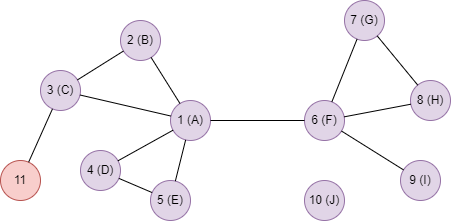
算法结果:每个点最多保留一个标签,返回 _uuid、label_1、score_1 三列
| _uuid | label_1 | score_1 |
|---|---|---|
| 1 | A | -0.200000 |
| 2 | F | -0.200000 |
| 3 | F | -0.200000 |
| 4 | F | -0.200000 |
| 5 | F | -0.200000 |
| 6 | A | -0.200000 |
| 7 | A | -0.200000 |
| 8 | A | -0.200000 |
| 9 | A | -0.200000 |
| 10 | J | 1 |
| 11 |
算法统计值:标签数量 label_count
| label_count |
|---|
| 3 |
命令和参数配置
- 命令:
algo(hanp) params()参数配置项如下:
| 名称 | 类型 |
默认值 |
规范 |
描述 |
|---|---|---|---|---|
| loop_num | int | 5 | >= 1 | 算法迭代轮数 |
| node_label_property | @<schema>.<property> |
/ | 数值或字符串类的点属性,需LTE | 作为标签的 schema 及属性名称;无该属性的点不参与计算;忽略时使用随机数作为节点的标签 |
| edge_weight_property | @<schema>.<property> |
/ | 数值类的边属性,需LTE | 边权重所在的 schema 及属性名称;无该属性的边不参与计算;忽略表示权重为 1 |
| m | float | / | 必填 | 邻居节点度的幂指数,表示对邻居节点度的偏向性;m = 0 代表不考虑邻居的节点度,m > 0 代表偏向节点度高的邻居,m < 0 代表偏向节点度低的邻居 |
| delta | float | / | (0,1);必填 | 传播中标签分值衰减因子 |
| limit | int | -1 | >= -1 | 需要返回的结果条数,-1 或忽略表示返回所有结果 |
示例:运行 HANP 算法,标签所在属性为 @default.label,边权重所在属性为 @default.level,幂指数为 0.1,标签分值衰减因子为 0.2,迭代 10 次
algo(hanp).params({
loop_num: 10,
node_label_property: "@default.label",
edge_weight_property: "@default.level",
m: 0.1,
delta: 0.2
}) as a return a
算法执行
任务回写
1. 文件回写
配置项 |
各列数据 |
|---|---|
| filename | _id,label_1,score_1 |
示例:运行 HANP 算法,标签所在属性为 @default.label,边权重所在属性为 @default.level,幂指数为 0.1,标签分值衰减因子为 0.2,迭代 10 次,将算法结果回写至名为 hanp 的文件
algo(hanp).params({
loop_num: 10,
node_label_property: "@default.label",
edge_weight_property: "@default.level",
m: 0.1,
delta: 0.2
}).write({
file:{
filename: "hanp"
}
})
2. 属性回写
配置项 |
回写内容 | 类型 |
数据类型 |
|---|---|---|---|
| property | label_1,score_1 |
点属性 | 标签的数据类型为 string,标签分值的数据类型为 float |
示例:运行 HANP 算法,标签所在属性为 @default.label,所有边权重为 1,幂指数为 0.1,标签分值衰减因子为 0.2,迭代 10 次,将算法结果分别回写至名为 tag_1、score_1 的点属性
algo(hanp).params({
loop_num: 10,
node_label_property: "@default.label",
m: 0.1,
delta: 0.2
}).write({
db:{
property: "tag"
}
})
3. 统计回写
| 统计项名称 | 数据类型 | 描述 |
|---|---|---|
label_count |
int | 标签个数 |
标签个数是指算法结束时,图中剩余标签的个数;HANP 算法只为每个节点保留一个标签,因此标签个数即为社区个数。
示例:运行 HANP 算法,标签所在属性为 @default.label,所有边权重为 1,幂指数为 0.1,标签分值衰减因子为 0.2,迭代 10 次,将算法统计值回写至任务信息
algo(hanp).params({
loop_num: 10,
node_label_property: "@default.label",
m: 0.1,
delta: 0.2
}).write()
直接返回
别名序号 |
类型 |
描述 | 列名 |
|---|---|---|---|
| 0 | []perNode | 点及其各标签、标签分值 | _uuid, label_1, score_1 |
| 1 | KV | 标签个数 | label_count |
示例:运行 HANP 算法,标签所在属性为 @default.label,所有边权重为 1,幂指数为 0.1,标签分值衰减因子为 0.2,迭代 10 次,将算法结果和统计值分别定义为别名 results 和 count 并返回
algo(hanp).params({
loop_num: 10,
node_label_property: "@default.label",
m: 0.1,
delta: 0.2
}) as results, count
return results, count
流式返回
别名序号 |
类型 |
描述 | 列名 |
|---|---|---|---|
| 0 | []perNode | 点及其各标签、标签分值 | _uuid, label_1, score_1 |
示例:运行 HANP 算法,标签所在属性为 @default.label,所有边权重为 1,幂指数为 0.1,标签分值衰减因子为 0.2,迭代 10 次,返回结果并按照标签名称和点的 UUID 升序排列
algo(hanp).params({
loop_num: 10,
node_label_property: "@default.label",
m: 0.1,
delta: 0.2
}).stream() as res
return res order by res.label_1, res._uuid
实时统计
别名序号 |
类型 |
描述 | 列名 |
|---|---|---|---|
| 0 | KV | 标签个数 | label_count |
示例:运行 HANP 算法,标签所在属性为 @default.label,所有边权重为 1,幂指数为 0.1,标签分值衰减因子为 0.2,迭代 10 次,返回社区数量
algo(hanp).params({
loop_num: 10,
node_label_property: "@default.label",
m: 0.1,
delta: 0.2
}).stats() as count
return count
结果一致性
受节点顺序、同权重标签随机选取、并行计算等因素的影响,HANP 算法的社区划分结果可能会不同。
