图数据库作为新兴的技术，已经引起越来越多的人们关注。近来，笔者收到很多朋友的提问，诸如如何看懂评测报告内的门门道道？如何通过评测报告，知晓各个产品间的优势和劣势？一个完备的评测报告需要哪些性能测试内容？哪些内容是考验性能的硬核标准？哪些可以忽略不计，如何去伪存真……

为了便于大家理解，本文第一部分先介绍关于图数据库、图计算与分析中的基础知识，第二、三部分进行图数据库评测报告的解读以及兼论图计算结果正确性验证。

一 | 基础知识

图数据库中的操作分为两类：

1. 面向元数据的操作，即面向顶点、边或它们之上的属性字段的操作；操作可以具体分为增、删、改、查四类。
2. 面向高维数据的操作，这也是本文关注的重点，例如面向全图或子图数据的查询结果返回多个顶点、边组合而成的高维数据结构，可能是多顶点的集合、点边构成的路径、子图（子网）甚至是全图遍历结果。

面向元数据的图数据库操作和关系型数据库有相似的地方，正确性验证方法在此不再赘述。本文着重在图数据库特有的高维数据查询正确性验证上。

面向高维数据的查询有三大类，它们也在所有基准测试报告中最为常见的：

1. K邻查询：即返回某顶点的全部K度（跳）邻居顶点集合。K邻查询可以有很多变种，包括按照某个特定方向、点边属性字段等进行过滤。还有全图K邻查询，也被视作一种高计算复杂度的图算法。
2. 路径查询：常见的有最短路径、模板路径、环路路径、组网查询、自动展开查询等。
3. 图算法：图算法在本质上是面向元数据、K邻、路径等查询方式的组合。

在大多数的基准测试报告中都不会说明是以何种方式实现以上的高维数据查询。在此，我们做个明确的说明，无论以何种方式进行高维查询，图数据库中的操作无外乎遵循如下3种遍历模式：

1. 广度优先（BFS）：例如K邻查询、最短路径就是典型的广度优先遍历模式。
2. 深度优先（DFS）：例如环路查询、组网查询、模板路径查询（含权重路径查询）、图嵌入随机游走等。
3. 以上两者兼而有之：以最短路径方式遍历的模板路径或组网查询、带方向或条件过滤的模板K邻查询、定制化的图算法等。

配图1中展示了BFS与DFS之间的差异。简而言之，在BFS模式下，如果不完成对第一跳邻居的穷举式遍历就不会开始对第二跳邻居的遍历，并依此类推直至完成对预定深度的完全遍历。因此，像K邻或最短路径查询，如果只能统计并返回限定数量的结果（例如1个邻居或1条路径），几乎可以判定其算法实现错误。

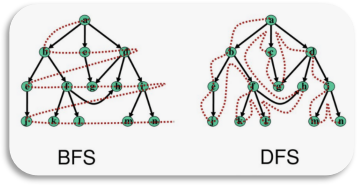
图1：广度优先遍历 vs. 深度优先遍历

基准测试数据集的选取一般分为三大类：

1. 社交或路网类数据集：像各图数据库厂商的基准性能评测中常用的Twitter-2010就是典型的基于社交图谱而形成的图数据集，其它的还有Amazon的电商社交数据集等。加州大学伯克利分校的GAP项目中用到的数据集则均属于路网（道路或Web）拓扑结构类数据集。
2. 合成数据集：像高性能计算组织Graph-500发布的一些数据集就是典型的人工合成数据集。国际标准化组织LDBC的SNB（Social Network Bench）测试中所用的数据集就是典型的合成的具有社交属性的数据集。
3. 金融场景数据集：像阿里妈妈基于其自身电商数据脱敏后公布的电商交易数据集，以及LDBC正在筹划推出的FB（FinBench）也属于典型的适配金融场景的（合成的）数据集。

注：随着图数据库、图计算的蓬勃发展，有理由相信更多类型、场景的适合基准测试、性能评测的图数据集会浮出海面。

下面，笔者以各图数据库厂商的基准性能评测中常用的Twitter-2010数据集为例，来说明如何进行图上查询的正确性验证。

Twitter数据集（其中顶点数量约4200万，边数量14.7亿，原始数据24.6GB）下载链接：http://an.kaist.ac.kr/traces/WWW2010.html

以Twitter数据集为例，了解一下图数据模型的特征：

• 有向图：由顶点（人）和边（关注关系）组成，其中关注关系为有向边。Twitter源数据中有两列，对应在每一行是由TAB键分割的两个数字，例如，12与13，代表两个用户的ID，表示两者间的有向的关注关系：12关注13。在图数据建模中就应该构建为两条边，一条表示从12到13的正向边，另一条则是从13到12的反向边，缺一不可。后面的验证细节中很多正确性的问题都与此相关——没有构建反向边，查询结果就会不可避免的错误。
• 简单图vs.多边图：如果一对顶点间存在超过（含）2条边，则其为多边图，否则即为简单图。在简单图中任意顶点间最多只有1条边，因此简单图也称作“单边图”。Twitter数据实际上是一种特殊的多边图，当两个用户互相关注对方时，他们之间可以形成两条边。在金融场景中，如果用户账户为顶点，转账交易为边，两个账户之间可以存在多笔转账关系，即多条边。很多系统只能支持简单的单边图，就会带来很多图上查询与计算的结果错误的问题。
• 点、边属性：Twitter数据本身除了隐含的边的方向可以作为一种特殊的边属性外，并不存在其他点边属性。这个特征区别于金融行业中的交易流水图——无论是顶点还是边都可能存在多个属性，可以被用来对实体或关系进行精准的查询过滤、筛选、排序、聚合运算、下钻、归因分析等。不支持点边属性过滤的图数据库可以认为功能没有实现闭环，也不具备商业化价值。

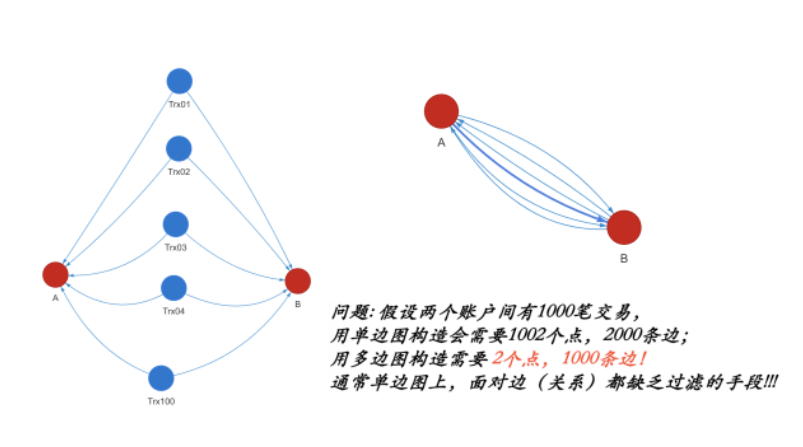
图2：单边图 vs. 多边图

二| 报告解读

图数据库基准测试报告的内容都会至少覆盖如下几个部分：

1. 测试环境：基准测试软硬件环境，测试数据集等；
2. 数据加载：全量数据加载、数据库启动效率等；
3. 查询性能：例如元数据、K邻、最短路径、图算法等；
4. 实时更新：对图数据的拓扑结构或元数据进行更新后的查询结果验证；
5. 功能完整性、易用性等：例如系统运维、灾备、监控、编程语言、二次开发接口等。

前面3个部分几乎所有厂家的基准测试报告都会覆盖，然而第4和第5个部分很多厂家就不会涉及——其中第4部分的有无可以看作是区分OLTP/HTAP与OLAP系统的最主要因素。区分一款真正的图数据库与图计算框架（或图数仓）的重要能力指标就是：系统是否具有实时、动态数据更新的能力——换言之，图数据库与图计算框架在是否支持实时更新上有本质的区别，前者可以数据动态更新，并在数据保持一致性的前提下支持各种图查询与算法，而后者则只能在静态的数据上做查询与更新（或者是每次更新后需要重新加载数据才能实现更新后的图查询与图算法计算）。

（一）测试环境

在具体的服务器指标上，不同的基准测试会存在差异，主要在计算、内存、外存和网络带宽上。这其中最核心的指标是服务器的CPU核数。采用CPU核数越高的系统说明该系统的潜在并发能力越高，反之则说明该系统并不会去充分释放CPU多核的并发算力。高性能系统通常会采用16核（32线程）以上的服务器实例进行测试。例如Neo4j系统，即便是其企业级安装也只需要8核CPU，因为Neo4j在绝大多数的查询和图算法计算过程中并发规模很低（每个查询的最大并发只能使用4线程）。类似的，基于Java编程语言或串行编程方式构建的图数据库系统都存在类似的特点——并发规模不高，系统性能、吞吐率不高、时耗大，因此一般测试服务器的核数都偏低（例如12核）。

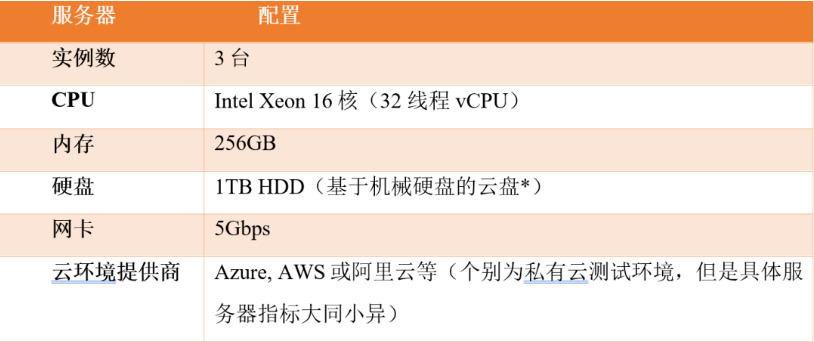
上表中列出的就是一种典型的中等配置的硬件环境。除了CPU的核数多少之外，内存、外存与网卡的性能也会对测试结果有一定的影响，但是它们在多数的图数据库性能测试项中并不是首要决定因素！这也是图数据库的基准测试与其它数据库差异最大的地方：图数据库是计算优先（计算与存储同为一等公民），而关系型数据库、数仓、数湖以及绝大多数分布式关系型数据库都是存储优先的（算力是附着于存储的二等公民）。换言之，传统数据库解决的是I/O或存储密集型挑战，而图数据库解决的是计算密集型挑战。

软件环境目前已知的所有图系统都基于Linux操作系统，并且会包含容器或虚拟化环境来进行封装与隔离。

（二）数据加载

• 数据集的大小、复杂度
• 加载时间
• 存储空间

其中，数据集大小关注的主要是点、边的数量以及复杂度。通常为了模拟接近真实商业场景，数据集的大小都在千万到十亿的量级（注：以国民经济中占比最大的金融服务行业为例，全国工商图谱、各家银行交易流水所构成的图数据集的规模基本就在百万到百亿级的量级）。复杂度一般会采用图的密度或点边数量比。图的密度对于有向简单图而言等于

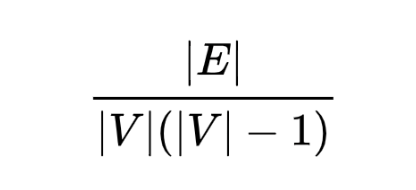
其中，V为顶点的数量，E为边的数量，图的密度最大为1。但是，实际上很多工业界的图并不是简单图，而是多边图，即一对顶点间可能存在多条边，密度公式并不适用，因此用点边比来表达更为简洁，即边的数量除以点的数量=（|E|/|V|）。以Twitter-2010数据集为例，其点边比=35.25（密度为0.000000846），通常点边比大于10的图数据集，进行深度挖掘或遍历时的挑战就更容易出现指数级计算复杂度增加的挑战。

加载时间和存储空间分别可以表示一款图数据库系统需要多久才能全量加载被测试的图数据集，以及加载完成后其所需要的持久化存储空间。加载时间可以显示一款图数据库系统的数据吞吐能力，越短越好。而存储空间占用则显示其对于资源占用的情况，不同的系统因为有不同的数据存储与计算结构设计思路，空间占用情况可能会存在巨大的差异——这也是NoSQL系统或分布式系统遵循去正则化（去归一化）原则的一个特点，通过存储多份拷贝，包括分片、分区等技术来实现更高效的计算效率与高可用性。

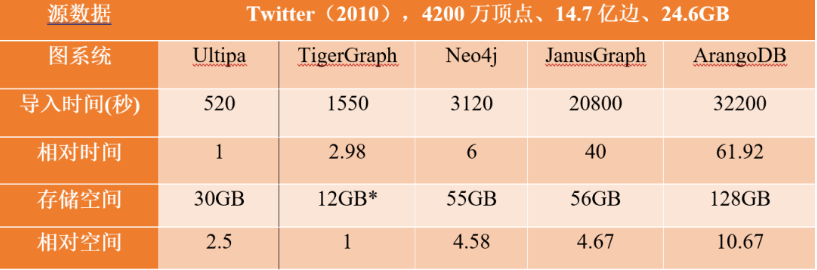
注：Tigergraph默认只对Twitter数据集进行了单向边存储，因此其存储空间占用节省了至少50%以上，如果完整的进行双向边存储，其存储空间消耗至少在24GB以上（导入时间也会翻倍）。关于单向边vs.双向边存储逻辑，在后面的正确性验证部分有详细论述。

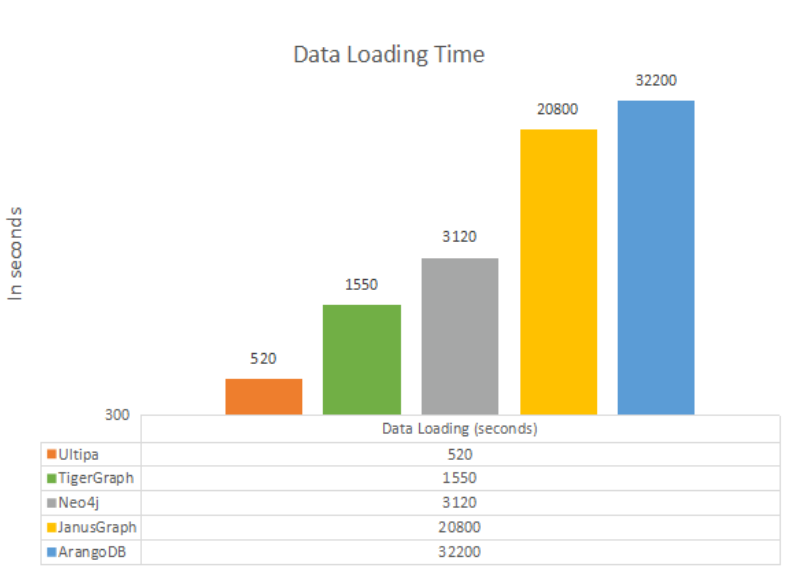
图3：图数据库的数据加载时间对标（示意图）

（三）查询性能

• 邻居查询：即K邻查询；
• 路径查询：通常为最短路径查询；
• 图算法：通常有PageRank、CC、LPA、相似度等算法，部分能力较强的图数据库会在大数据集上运行Louvain社区识别类复杂算法。

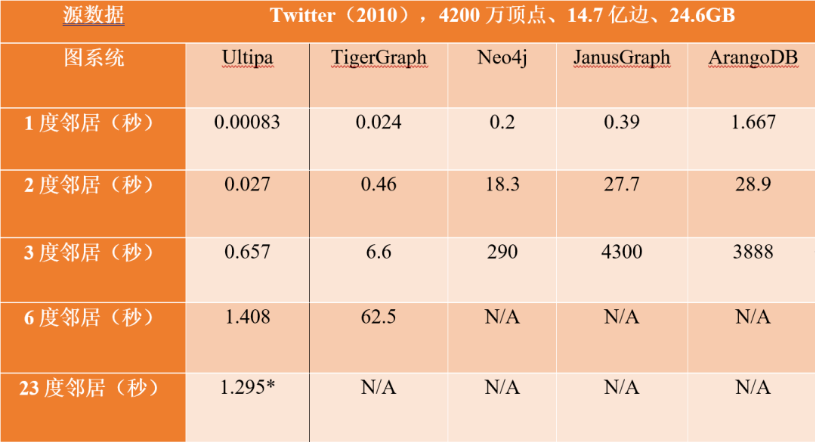
K邻查询通常会探测不同的遍历深度条件下的时耗，以Twitter数据集为例，一般会遍历1度到6度的邻居，并通过比较时耗来进行直接对标。通常1度邻居各家都可以做到秒级（2秒以内），快一些的图数据库会在毫秒级（<30毫秒）甚至微秒级（<1毫秒）。但是，2度邻居开始，因为计算复杂度的指数级增加，极少有系统可以做到毫秒级（如下表所示），而6度邻居能做到秒级（<10秒）的系统，绝对可以看作是实时图数据集，因为6跳查询基本上是对全部点边（15亿的量级）进行了完全遍历。

K邻查询的效率和数据加载的正确性与否，以及查询方式的正确性与否直接相关，在后面的正确性验证部分，我们会详细分析各家评测报告中可能出现的错误。最典型的错误就是只进行了部分查询，结果错误，但是查询时间显得很短，因此在基准测试报告中，必须要体现结果，例如每个顶点的K跳邻居的具体个数！

、

注：Ultipa在Twitter数据集上进行了超深度遍历效果的公布。因为Twitter数据集只存在1个联通分量（即全部顶点都有路径相连），但是有的顶点的邻居可以最远距离达到了23层（度）以上，这种超深度的遍历体现了一个图数据库系统的深度下钻的能力，传统意义上，Twitter数据遍历在3层（含）以上对很多系统就已经非常吃力，时耗很大（以分钟甚至小时计）。

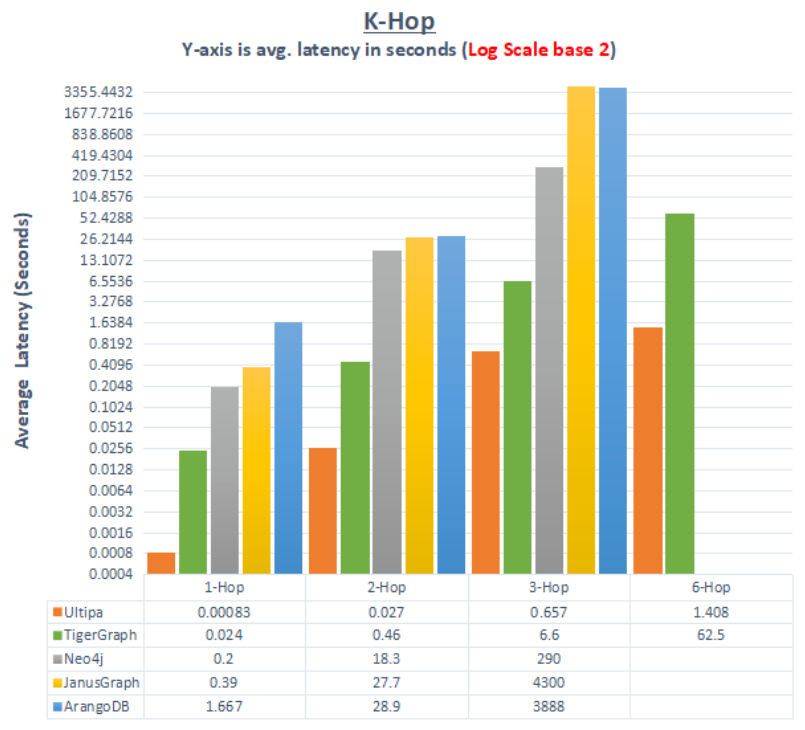
图4:图数据库的邻居查询时间对标（示意图）

最短路径查询测试的是图系统在数据集中遍历寻路的能力。最短路径是K邻查询的一个变种，它相当于是固定了起点与终点，并寻找它们之间的全部可能的最短路径（区别于K邻查询是只固定顶点，要找到全部的满足遍历深度条件的终点集合）——这其中最重要的限定条件是返回全部的路径，在连通度较高的Twitter数据集中，很多顶点间的最短路径数以百万计！目前为止只有3家图数据库厂家公布过它们在Twitter数据集上的最短路径评测结果，但只有Ultipa公布过最短路径的数量（如下表所示）。有一些图数据库系统仅返回1条最短路径，这显然是过于学术化的最短路径图遍历实现方式——在金融服务场景中，例如持股关联路径、交易流水、反洗钱路径，显然需要穷举找到全部可能的路径，而且速度越快越好。

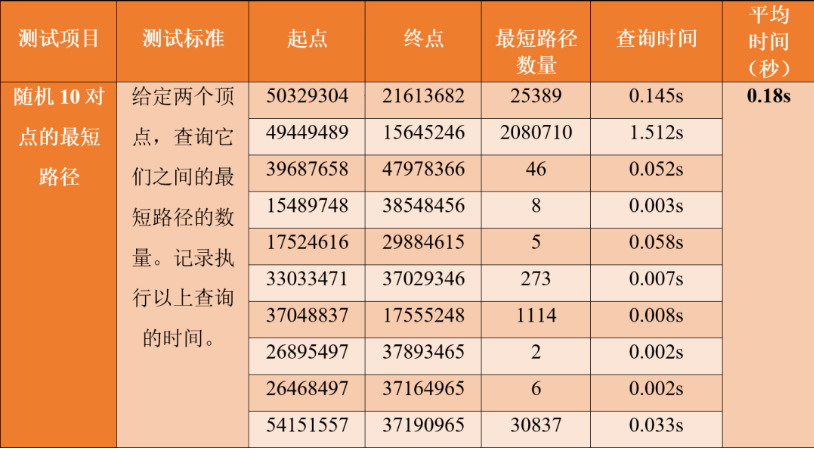
图算法体现的是一个图数据库系统对全量数据的高效、迭代、遍历处理能力。支持的图算法的多少能体现系统功能的丰富度，而时耗指标则最直接的反映出该系统的性能。但是，大部分的图数据库系统集成的是某种图计算引擎或框架，它只能处理完全静态的数据，一旦数据产生变化后，只有经过重新的全量数据映射后，图算法运行结果才会发生改变。像Neo4j、Spark GraphX就属于这种情况。因此在对标测试时，还需要观察数据变动后，图算法的计算结果是否产生相应变化。

PageRank算法是最知名的一种图算法，得名于谷歌的联合创始人Larry Page，也是在互联网搜索引擎中进行网络排序的核心算法。PageRank也是最早被用在大规模分布式系统中的一种逻辑相对简单，容易实现分布式计算的图算法，因此所有的图数据库、图计算厂家都会提供该算法。PageRank算法逻辑虽然简单，但是还有很多细节应该体现在基准测试中，例如其计算结果是否可以支持数据库回写、文件回写、流式返回、结果排序。在真正的商业化对标测试中，通常会有两点：

• 必须对全量数据进行迭代计算；
• 对结果进行排序，并返回Top-N的结果进行比对。

以上两点缺一不可。我们发现有些系统竟然只对部分数据进行局部计算，这个直接违背了PageRank的全局迭代计算的算法本质，Neo4j就是一个典型的例子，如果在算法调用传参中限定返回1000，则它居然只计算1000个顶点的PageRank值，如果全量数据是Twitter，这个结果100%是错误的，它相当于只进行了全量数据的四万分之一的计算。另外，结果是否支持排序，如果数据库不支持排序，就相当于把这个压力直接转移给了业务层（应用层），这个能力直接反映了一款图数据库的设计与实现能力。多数图数据库的基准测试中如果不提及这些问题，其结果的可信度则大打折扣。

下表中列出了PageRank图算法的测试逻辑、返回结果的Top-10，以及运行时间。

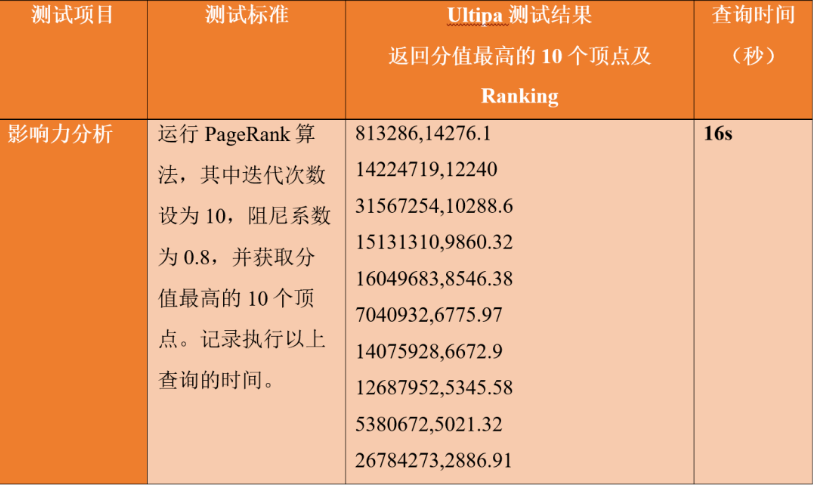
LPA（标签传播）算法是一种典型的社区识别算法，以标签分布达到稳定为目标的一种对顶点进行聚类的迭代算法，较PageRank而言算法复杂度更高，耗时也相对而言更高(通常是PageRank算法的数倍)，它会返回社区数量，但算法结果可能会存在一定随机性（例如对于一个顶点而言，当其邻居顶点的多个标签的综合权重相等时，会随机选择其中一个标签，这种随机性会导致最终结果的随机性）。LPA与PageRank类似，对它的调用也涉及到各种回写与返回结果设定。LPA算法有很多的变种，例如单一标签传播、多标签传播等，多标签传播的实现复杂度要较单一标签复杂得多，因此基准测试中一般采用单一标签传播。

鲁汶社区识别算法（Louvain）是一款基于模块度（modularity）计算的社区识别算法，以最大化模块度为目标的一种对顶点进行聚类的迭代算法。鲁汶社区识别算法的计算复杂度较LPA相比更高，因此很少有图数据库厂家在点边规模1亿以上的图数据集上进行鲁汶算法的性能评测。鲁汶算法的最早的原生实现是串行的方式，虽然是C++实现的，在10亿量级的数据上面也需要2.5个小时完成，如果用Python来实现，需要至少几百个小时（几周的时间）。目前已知的在10+亿级大图上的鲁汶社区识别只有Ultipa系统公开过相关性能测试数据。和LPA算法结果中可能出现随机性的逻辑一样，鲁汶算法结果中的模块度（及对应的社区数），也可能会出现抖动，这种抖动与具体数据集的拓扑结构直接相关。

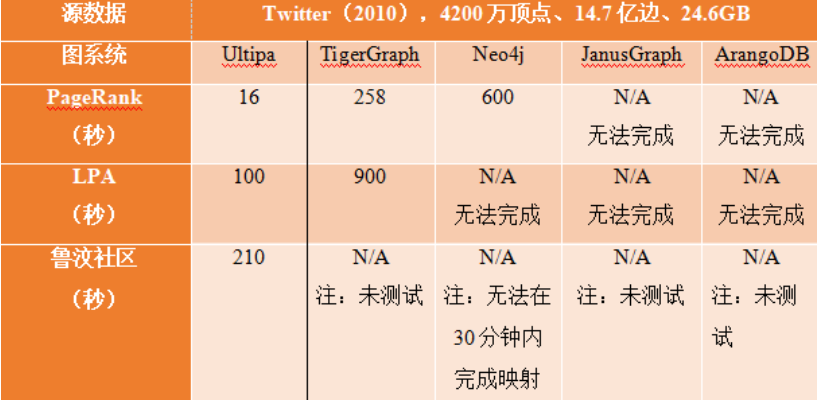
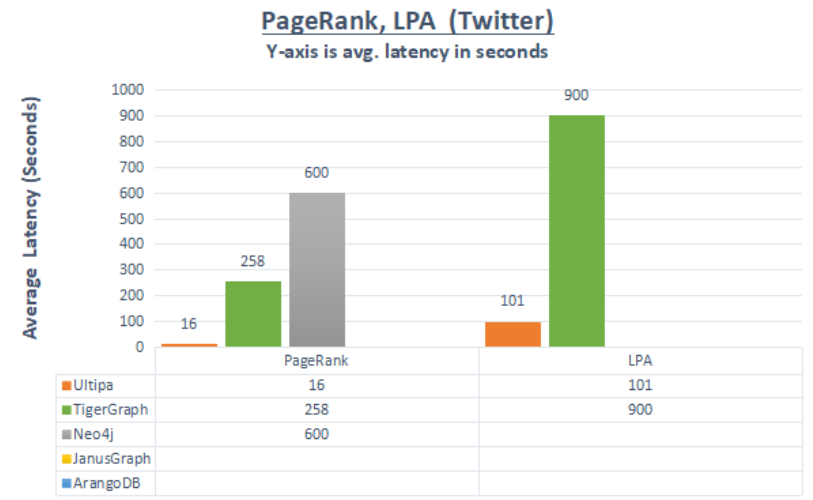
图5:图算法查询时间对标（PageRank & LPA）

(四)实时更新

• 只面向元数据（TP）：这个操作只影响点、边或其属性字段，从传统数据库视角看属于一种事务性操作（ACID），在图数据库里面还可能代表着图的拓扑结构的变化——例如修改、增加或删除一条边、一个顶点都会导致图的拓扑结构变化；
• 更新元数据后，运行图查询或算法（TP+AP）：这个属于一种复合操作，它实际上代表的是当图的拓扑结构产生变化后，在进行图查询（K邻、路径等）或图算法计算时，是否能实时的反映出结果变化。

实时更新一方面可以看元数据更新时的延迟与TPS（或QPS），另一方面可以检查图查询的结果在元数据更新前后的变化情况以及相应查询的QPS。很显然，这对于图数据库的要求是它有能实时更新+实时查询的能力。目前为止，在基准测试中发布相关信息的产品只有Ultipa图数据库发布了在Twitter数据集上面的相关结果。

下面的例子中展示的就是把某个顶点的第K度（跳）邻居之一与其通过一条新建的边相连后，再次查询其K邻后的结果变化情况。如果是静态数据库、静态图谱，增加边后，K邻结果会保持不变（错误）。

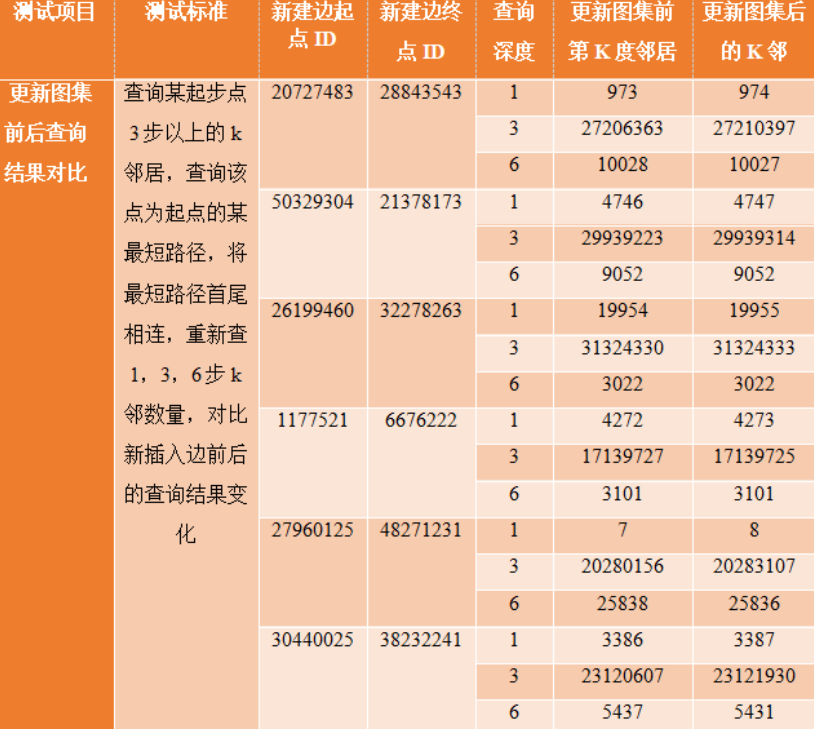
三 | 正确性验证

本节中着重说明如何对3大类型查询进行正确性验证：

• K邻
• 最短路径
• 图算法

我们先以K邻查询为例来验证图数据库查询结果正确性。

首先，要明确K邻查询的定义，事实上K-Hop查询有两种涵义，分别是：

1. 第K度（跳）邻居
2. 从第1跳到第K跳的全部邻居

其中第K跳邻居指的是全部距离原点最短路径距离为K的邻居数量。以上两种涵义的区别仅仅在于到底K-Hop的邻居是只包含当前步幅（跳、层）的邻居，还是要包含前面所有层的邻居。

无论是哪种定义，有两个要点直接影响“正确性”：

1. K邻查询的正确实现方式默认应基于广度优先搜索！
2. 结果集去重：即第K层的邻居集合中不会有重复的顶点，也不会有在其它层出现的邻居！（已知的多个图数据库系统都存在数据结果没有去重的错误。）

有的厂家会用深度优先搜索（DFS）的方式，通过穷举全部可能的深度为K跳的路径来试图找到全部途径和最终能抵达的终点。但是，DFS方式实现K邻查询有2个致命的缺点：

1. 效率低下：在体量稍大的图中，不可能遍历完毕，例如Twitter数据集中常见的有超过百万邻居的顶点，如果以深度遍历的复杂度是天文数字级的（百万的11次方以上）；
2. 结果大概率错误：即便是可以通过DFS完成遍历，也没有对结果进行分层，即无法判断某个邻居到底是位于第1跳还是第N跳。

下面我们再举两个有代表性的例子：

• 最短路径
• 图算法

最短路径可以看作是K邻查询的一个自然的延展，区别在于它需要返回的结果有两个特征：

• 高维结果：最短路径需要返回的多条由顶点、边按遍历顺序组合而成的路径；
• 全部路径：任意两个顶点间可能存在多条最短路径，如果是转账网络、反洗钱网络、归因分析等查询，只计算一条路径显然是无法反映出全貌的！

我们先从验证1度（1跳）邻居开始,以Twitter数据集的顶点“27960125”为例，在源数据集中，如下图所示，返回了8行（对应图数据库中的8条边！），但是它的1度邻居到底是几个呢？

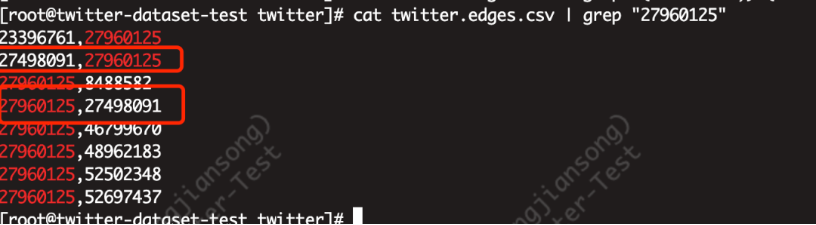
图6：Twitter源数据中顶点关联的边

正确的答案是：7个！注意上图中顶点27960125的一个邻居27498091出现了2次，它们之间存在两条相互关系（对应源数据中的2行），但是作为去重的1度邻居集合，只有7个。

为了更精准地验证结果正确性，对K邻查询还可以按照边的方向来进行过滤，例如只查询顶点“2796015”的出边、入边或者双向边（注：默认是查询双向边关联的全部邻居）。下图展示了如何通过图查询语言来完成相应的工作。注意，该顶点有6条出边对应的1跳邻居、2条入边对应的1跳邻居，其中有1个邻居“27498091”是重叠的。

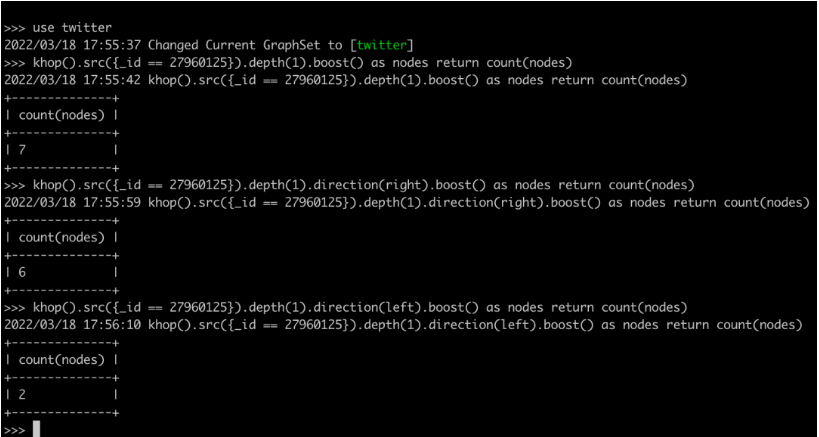
图7：命令行工具操作K邻的3种模式（Ultipa CLI）

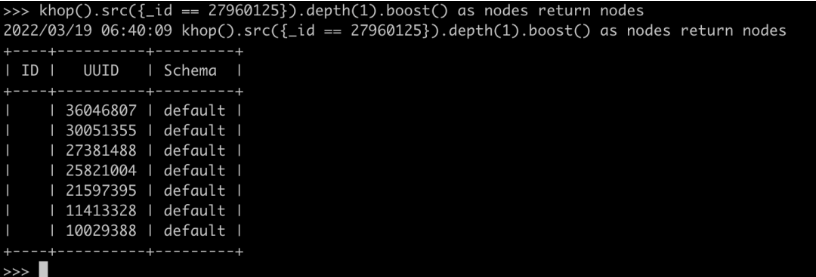
图8：命令行工具操作K邻返回结果集（Ultipa CLI）

以Tigergraph发布的性能评测报告数据为例，其结果集存在明显的、广泛的错误，顶点27960125的1-Hop结果仅返回6个邻居！（如下图所示）。

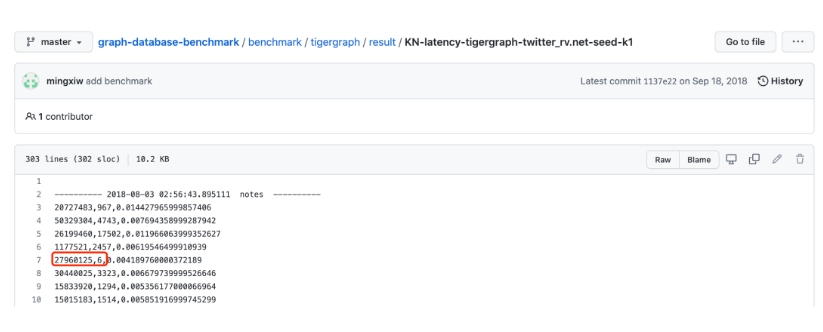
图9：Tigergraph的性能评测结果中的数据（参考Github公开的测试结果数据）

Tigergraph的查询结果错误有3个可能，都具有典型性：

• 构图错误：只存储了单向边，没有存储反向边，无法进行反向边遍历；
• 查询方式错误：只进行了单向查询，没有进行双向边遍历查询；
• 图查询代码实现错误：即没有对结果进行有效的去重——这个我们在多跳K-hop查询中再继续分析。

其中，构图错误代表着数据建模错误，这意味着业务逻辑不能在数据建模层面被准确反映。例如在反欺诈、反洗钱场景中，账户A收到了一笔来自账户B的转账，但是却因为没有存储一条从A至B的反向边而无法追踪该笔交易，这显然是不能容忍的。查询方式和查询代码逻辑错误同样也会对结果造成严重影响——每一跳查询双向边，在多跳情况下查询复杂度指数级高于单向边查询，这也意味着Tigergraph如果正确地实现图数据建模、存储与查询，其性能会指数级降低，并且存储空间的占用也会成倍增加（存储正向+反向边的数据结构要比仅存储单向边复杂2x以上），数据加载时间也会成倍增长。

如果我们继续追溯顶点“27960125”的2-Hop结果集，就会发现结果的错误会更加隐蔽，例如Tigergraph的2-hop实际上仅仅返回了沿出边遍历的第二度的邻居结果，并且没有对结果去重。如下面2张配图所示，其第二度邻居数目1128中含有重复的顶点，按照其只进行出边查询得到的去重的结果应该是1127——但是2nd-hop的正确结果应该是533108！这两者间有473倍的差异，即47300%的误差！在2跳的结果中，就可以看到Tigergraph的查询结果同时存在以上所述的三种错误——构图错误、查询方式错误、结果未去重错误！

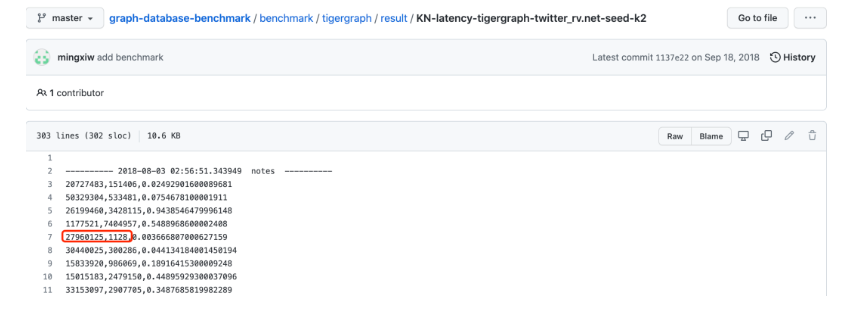
图10：Tigergraph的仅进行单向遍历的错误的2nd-Hop结果

遗憾的是，Tigergraph的查询结果错误问题在今天的图数据库市场并不是个例，我们在Neo4j、ArangoDB等系统中也发现因底层实现或接口调用等问题而出现的错误——更为遗憾的是，有多个厂家的“自研图数据库”实际上是对Neo4j社区版或ArangoDB的封装，姑且不论这么操作是否涉嫌违规商用，暴力封装几乎注定了它们的查询结果也是错误的。例如Neo4j默认并不对K邻查询结果进行去重，而一旦开启去重，它的运行效率会指数级下降，因此为了保证效率，K邻结果默认都是不去重的；而ArangoDB有一种最短路径查询模式，只返回一条路径，这种模式本身就是对最短路径的错误理解与实现。

、

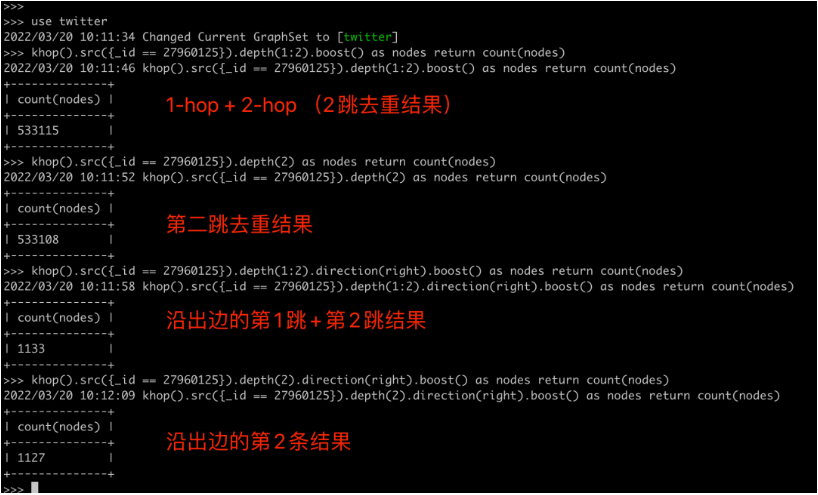图11：Ultipa的正确的K-Hop查询结果（4种查询方式）

可视化的工具可以帮助我们更直观、便捷地查询结果的正确性。

例如，某数据集中ID为“12242”的顶点的1度邻居查询，有12个邻居，在Ultipa Manager中操作结果如下：

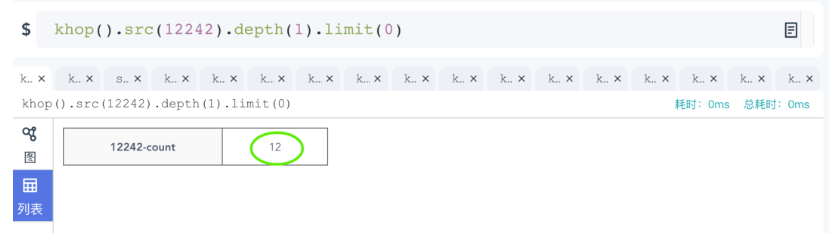
图12：Ultipa Manager中的K邻图查询操作示意图

如何可视化的验证结果正确性呢？可以通过对该顶点进行广度优先的展开操作，即展开其全部的边所关联的第一层（跳）的邻居。如下图所示，可以看到，尽管12242有18条边，但是关联的具有唯一ID的、去重后的邻居只有12个。

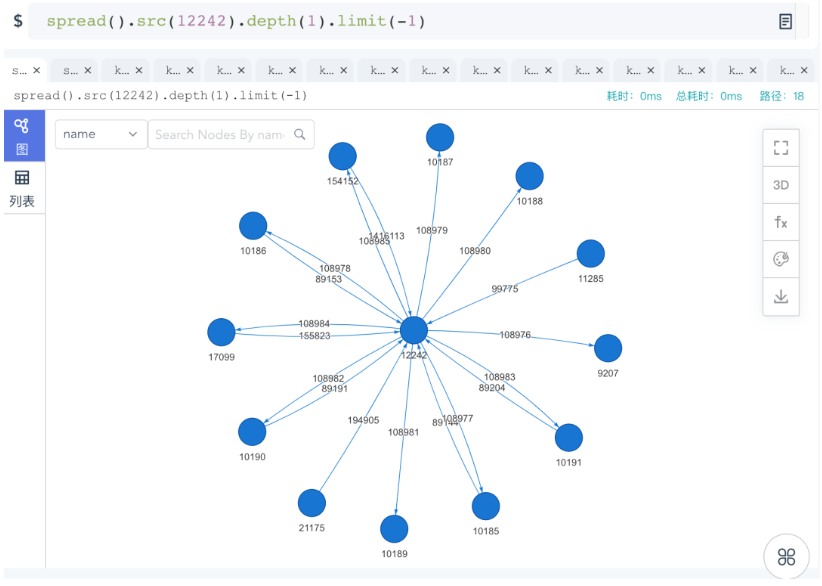
图13：Ultipa Manager中的自动展开图查询操作示意图

上面我们展示了图上的基础查询K邻查询的正确性验证方法，以及可能出现的错误情形。还有很多其它的图操作同样也涉及到结果错误的问题，但是都能通过一些基础的方法来验证结果正确性。

下面再举两个有代表性的例子：

• 最短路径
• 图算法

最短路径可以看作是K邻查询的一个自然的延展，区别在于它需要返回的结果有两个特征：

• 高维结果：最短路径需要返回的多条由顶点、边按遍历顺序组合而成的路径；
• 全部路径：任意两个顶点间可能存在多条最短路径，如果是转账网络、反洗钱网络、归因分析等查询，只计算一条路径显然是无法反映出全貌的！

图14:命令行工具最短路径结果返回（Ultipa CLI）

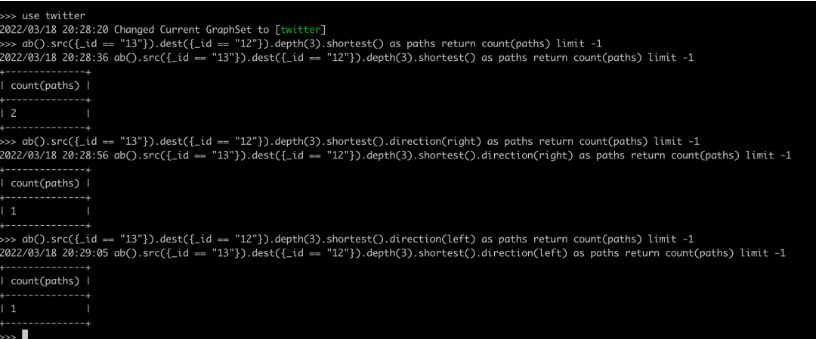
图15：最短路径查询的3种模式（Ultipa CLI）

以Twitter数据集中的顶点12、13之间的最短路径为例，我们发现它们之间存在2条最短路径，其中1条由12指向13，另一条由13指向12，这个在源数据中也可以通过“grep”操作得到快速的验证。在更复杂（更深度）的查询中，可以用类似的逻辑，通过层层的抽丝剥茧来验证结果的正确性。

下面我们以杰卡德相似度算法为例来说明如何验证图算法的正确性。以如下的一张非常简单的图（下左图）为例，计算红、绿两个顶点间的相似度，计算公式如下右图所示。图中，红、绿节点的共同邻居数为 2，全部邻居数合计为 5，我们可以手工推算出这两个节点的杰卡德相似度为 2 / 5 = 0.4。

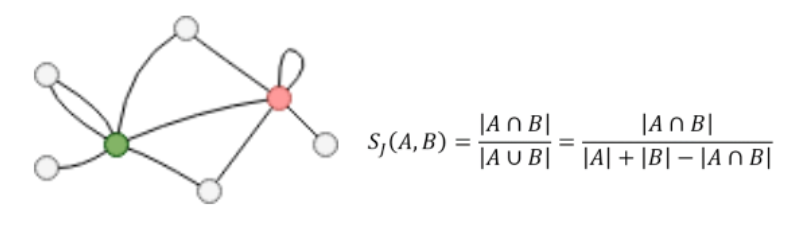
图16：杰卡德相似度示例数据集与计算公式

直接调用杰卡德相似度的算法的结果也应该是0.4（40%）。如果用图查询语言来白盒化的实现，代码逻辑如下：

图17：杰卡德相似度多句图查询语言实现（UQL）

在Twitter数据集中，任意两个顶点间的杰卡德相似度的计算的复杂度和被查询顶点的1度邻居的个数直接相关，以顶点12、13为例，它们都是典型的有百万邻居的“超级节点”，在这种情况下，手工验证结果的准确性并不现实。但是可以通过多组查询来校验记过是否正确，逻辑分为如下5步：

1. 运行杰卡德相似度算法(如下图所示）：

图18：杰卡德相似度算法调用（UQL）

2.验证方法一：通过多句查询计算杰卡德相似度（如下图所示）：

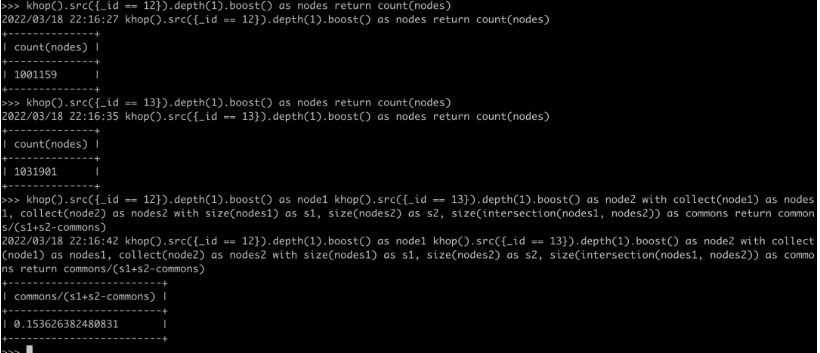
图19：杰卡德相似度算法验证方法一（UQL）

3.验证方法二：查询顶点12的1跳邻居个数（下图）：

4.验证方法二：查询顶点13的1跳邻居个数（下图）：

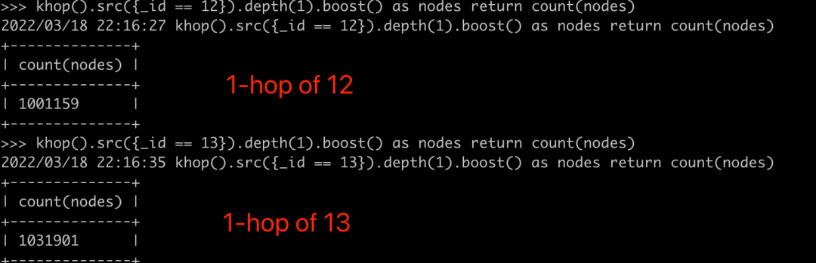
图20：杰卡德相似度算法验证方法二之第一部分（UQL）

5.验证方法二：查询顶点12到13之间的全部深度为2的路径（如下图）——这一结果就是两个顶点之间的全部共有邻居；

图21：杰卡德相似度算法验证方法二之第二部分（UQL）

6.验证方法二：用以上第5步的结果，除以（第3步结果 + 第4步结果 – 第5步结果）= 0.15362638；

7.如果以上算法和两种验证方法结果均一致，则图算法计算结果正确。

本文中，笔者详细地介绍了如何解读图数据库基准测试报告，并进行查询正确性验证的方法，让大家可以更好地了解图数据库，去伪存真。聪明的读者还可以开阔思路、举一反三！

最后，还有一个小知识分享，图数据库的英文为Graph Database，有一些朋友喜欢翻译为图形数据库或图形库，这是不可取的。图（Graph）一词源自图论（Graph Theory）,而图形则来自于Graphics，两者虽然词根相同，涵义不同——Graph指的是事物的集合及其拓扑结构与关联关系，而Graphics是平面设计或可视化图像。因此，叫做图形数据库并不准确。（ 来源：AI科技评论   文/ 教授老边  ）

链接：如何去伪存真地看懂一份图数据库的评测报告？