作者：孙宇熙

很多现实世界中的应用场景都可以用图来表达，特别是应用数据可以以网络化的模式来表达的时候，从交通道路网络、电话交换网络、电网、社交网络到金融交易网络。如果您没有关注过相关的领域，您可能会惊诧于图的技术得到了多么广泛的应用。业界很多赫赫有名的公司都是基于图技术而构建的，例如：

• 谷歌：PageRank 是一种大规模页面（或链接）排序的算法，可以说，早期谷歌的核心技术就是一种浅层的并发图计算技术。
• 脸书：脸书的技术框架的核心是它的 Social Graph，即朋友关联朋友再关联朋友。在任意两个人之间通过 5 或 6 个人就可以建立联系。脸书开源了很多东西，但是这个核心的图计算引擎与架构从未开源过。
• 推特：推特它曾经在 2014 年短暂的在 Github 上面开源了 FlockDB 项目，但随后就下线了，原因很简单，图计算是推特的商业与技术核心，开源模式没有增加其商业价值——换句话说，任何商业公司的核心技术与机密如果构建在开源之上，其商业价值形同虚设。
• 领英（LinkedIn）：领英是专业职场社交网络，特点是推荐距离你 2 层至 3 层的专家，提供这种推荐服务必须使用到图计算引擎（或图数据库）。
• 高盛集团：在 2007-2008 年爆发的美国次贷危机中，莱曼兄弟公司破产，而高盛集团全身而退，背后的真实原因是高盛集团拥有强有力的图数据库系统—— SecDB，它成功计算并预测到即将发生的金融危机。
• Paypal、E-bay和许多其他金融或电子商务公司：图计算可以帮助他们揭示出数据的内部关联，而传统的关系型数据库或大数据技术实在是太慢了，它们在设计之初就不是用来处理数据间的深度关联关系的。

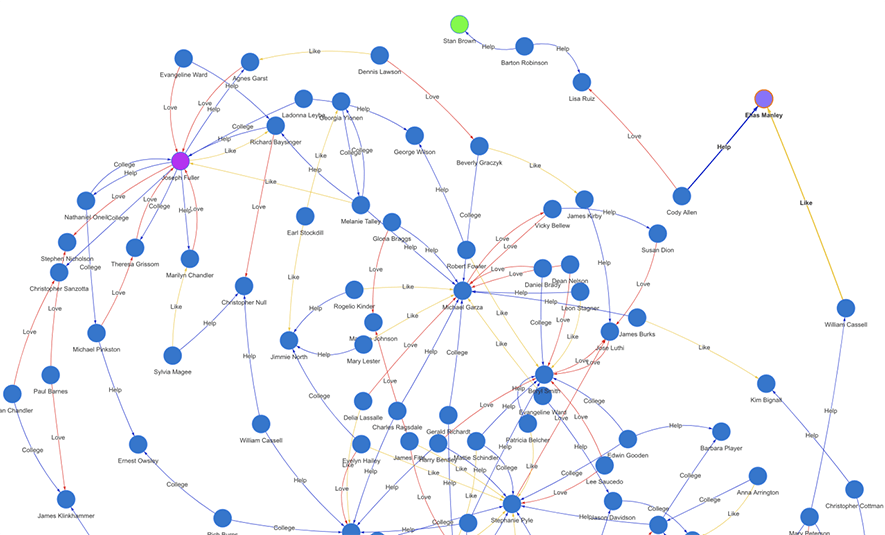
Diagram-0：典型的社交网络图谱（实时生成的子图）

上面这张配图（Diagram-0）展示了一个典型的社交图网络的局部。它实际上是在一张大图上进行的实时路径查询所生成的一张子图。绿色的节点为初始顶点，紫色的节点为终止顶点，两者间有 15 层间隔，并有 100 条关联路径，每条路径上有不同类型的边连接着相邻的两两的顶点，其中不同类型（属性）的边以不同的色彩来渲染，以表达不同类型的社交关系（帮助、喜欢、爱情、合作、竞争等等）。

图的数据结构大体包含 3 种类型的数据：

1. 顶点（vertex，复数：vertices），也被称作点、节点（node），顶点可以有多个属性，下面的边也一样，有鉴于此，某个类型的顶点的集合可以看作类似于传统数据库中的一张表，而顶点间的基于路径或属性的关联操作则可看作是传统关系型数据库中的表连接（table-join）操作，区别在于图上面的 join 操作的效率指数级高于 SQL;
2. 边（edge），也称作关系（relationship），一般情况下一条边会连接两个顶点，两个点的排列顺序可以表明边的方向，而无向边通常通过双向边来表达，所以 A-B = A↔B = A←B + B→A。而那种特殊类型的可以关联多个（>=3）顶点的边，一般都被拆解为两两顶点相连的多条边来表达；
3. 路径（path），表达的是一组相连的顶点与边的组合，多条路径可以构成一张网络，也称作子图，多张子图的全集合则构成了一张完整的图数据集，我们称之为“全图”。很显然，点和边这两大基础数据类型的排列、组合就可以表达图上面的全部数据模型。

图中的数据类型的表达：

• 顶点：v, v, w, a, b, c…
• 边：(u, v)
• 路径：(u, v), (v, w), (w, a), (a, j)… …

注意，上面的边的表达形式 (u, v) 通常代表有向边，也就是说边的方向是从 u 指向 v，我们也称 u 为 out-node（出点），v 为 in-node（入点）。无向图中的无向边通常通过双向有向边来表达，在数据结构中不同的设计方案有不同的表达方式，例如在二维相邻矩阵中，如果行、列相交的顶点中行 u 为出点，列 v 为入点，那么矩阵中的对应的交点表达的是从行出点 u 到列入点 v 的一条有向边，另一条反方向的边则是从行出点 v 到列入点 u 的有向边。而在下面将要介绍到的相邻哈希的数据结构中，这个表达相对更为简易，(u, v, 1) 和 (v, u, -1) 分别表达了 u→v 和 v→u 两条边。在相邻链表数据结构中，则从 u 出发存在最终指向 v 的某条链接（链路），反之亦然。之所以要表达反向边的一个原因是如果不存在从 v 到 u 的边，那么在图上（路径）查询的时候，将不会找到从 v 出发可以直接到达 u 的任何边，也就意味着图的连通度受到了破坏——或者说数据结构的表达没有反映出真实的顶点间的路网连接情况！

传统意义上，表达图的数据结构有两类:

• 相邻矩阵，源自英文 Adjacency Matrix
• 相邻链表，英文 Adjacency List

简单而言，相邻矩阵是一个二维的矩阵，在计算机科学语境下，一个二维数组中的每个元素都代表了图中是否存在着两个顶点之间的一条边。

相邻链表用了一种迥然不同的方式来表达图上的连接关系，如下图（Diagram-1）所示，左侧的有向（并带权重的边）图用右侧的相邻链表表达，它包含了第一层的“数组”其中每个元素对应图中的一个顶点，第二层则是每个顶点的边所直接关联的顶点构成的链表。注意，右侧的相邻表中只是表达了有向图中的单向边，如果从顶点 4 出发，只能抵达顶点 5，却无从知道顶点 3 可以抵达顶点 4，除非用全图遍历的方式搜索，那样的话效率会相当低下。当然，解决这一问题的另一种方式是在链表中也插入反向边和顶点，类似于上文中提及的相邻哈希中如何来表达反向边。

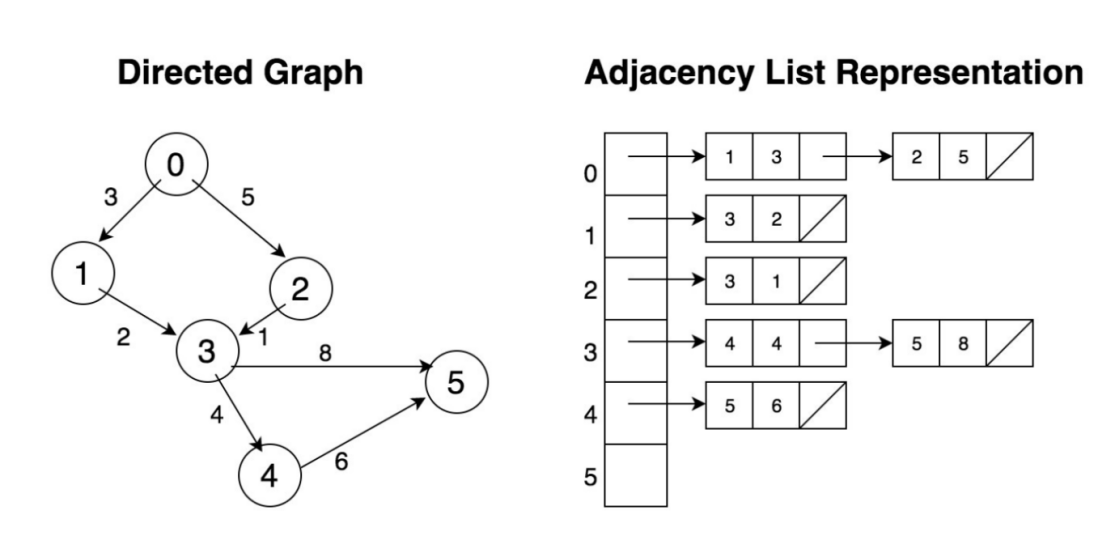
Diagram-1：用相邻链表来表达有向图（单向边）

如果 Diagram-1 中的有向图用相邻矩阵来表达，每条边需要用矩阵中的一个元素来对应行、列中一个顶点，其中矩阵是 6x6 的，并且其中只有 7 个元素（7 条边）是被赋值的。很显然，这是一个相当稀疏的矩阵，占满率只有 (7/36) < 20%，然而它所需要的最小存储空间则为 36 字节（每个字节可以表达每条边的权重）。如果是一张有 100 万顶点的图，其所需的存储空间至少为 100GB（1M*1M = 1万亿字节），而这在工业界中只是属于小图的范畴的。

Diagram-2：用相邻矩阵来表达有向图

也许读者会质疑以上相邻矩阵的存储空间的估算被夸大了，那么我们来探讨一下：如果每个矩阵中的元素可以用 1 个比特位来表达 ，那么 100 万顶点的全图存储空间可以降低到 125GB。然而，我们是假设用 1 个字节来表达边的权重，如果这个权重的数值范围超过 256，我们或许需要 2 个字节、4 个字节甚至 8 个字节，如果边还有其它多个属性，那么对于存储空间就会有更大的甚至不可想象的需求。

现代的 GPU 是以善于处理矩阵运算而闻名的，不过通常二维矩阵的大小被限定在小于 32K（32,768）顶点。这是可以理解的，因为 32K 顶点的内存存储空间已经达到 1GB+ 了，而这已经占到了 GPU 内存的 25-50%。换句话说，GPU 并不适合用做大图上面的运算，除非使用极其复杂的图上的 Map-Reduce 的方式来对大图进行切割、分片来实现分而治之、串行的或并发的处理方式——但是你真的觉得这种分片、切图的处理方式的效率会很高吗？

存储低效性或许是相邻矩阵最大的敌人。这也许可以解释为什么在学术界以外，尤其是工业界，很少用到真正意义上的相邻矩阵来对真实世界的问题进行数据建模。尽管它有着 O(1) 的访问时间复杂度。

相比而言，相邻链表对于存储空间的需求要小得多，在工业界中的应用也更为广泛。例如脸书的社交图谱（其底层的技术架构代码为 Tao/Dragon）采用的就是相邻链表的方式。链表中每个顶点表示一个人，而每个顶点下的链表表达的是这个人的朋友或关注者。这种设计方式很容易被理解，但是它可能会遇到热点处理效率的问题，例如如果一个顶点有 1 万个邻居，那么链表的长度有 10,000 步，遍历这个链表的时间复杂度用 Big-O Notation 来表达为 O(10,000)。在链表上的增删改查的操作都是一样的复杂度，更准确的说，平均复杂度为 O(5,000)。另一个角度来看，链表的并发能力很糟糕，你无法对于一个链表进行并发（写）操作！

现在，让我们思考一个方法，一种数据结构可以平衡两件事情：

• 存储空间：相对而言可控的、占用更小的存储空间来存放更大量的数据  
• 访问速度：低访问延迟，并且对于并发访问友好

在存储维度，我们要尽量避免使用那种稀疏的，利用率低下的数据结构，因为大量的空数据占用了大量的空闲空间，以相邻矩阵为例，它只适合用于那种拓扑结构非常密集的图，例如全联通图（所谓全联通指的是图中任意两个顶点都直接关联）上面提到的 6 顶点的图，如果全部联通，则至少存在 30 条有向边 = 2*6*5/2，如果还存在自己指向自己的边，或顶点对间存在多条边，则存在至少 36 条边，那么用相邻矩阵表达的是数据结构是节省存储空间的。然而，实际应用场景中，绝大多数的图都是非常稀疏的（我们用图的密度 = (边数/全联通图的边数) * 100% 来衡量，大多数图的密度远低于 5%），因此相邻矩阵就显得很低效了。

相邻链表在存储空间上是大幅节省的，然而链表的设计存在访问延迟大，并发访问不友好等问题，因此突破点应该在于：如何取代链表为中心的数据结构设计方式。

在这里，我们设计并命名了一种新的数据结构：相邻哈希（英文：Adjacency Hash 或 Adjacency Hash<*>）。它具有如下的特点：

• 定位图中任意顶点的时耗恒定为 O(1)
• 定位图中任意边的延迟为 O(2)

以上时耗的复杂度假设可以通过某种哈希函数来实现，最简单的例如通过数组下标访问具体的点、边元素来实现，对于边而言仅需定位 out-node+in-node，时耗为 O(1+1)。

在 C++ 中，面向以上的特点的数据结构，最简单粗暴的实现方式为，动态向量数组（Array of Vectors）：

// Array of vectors

Vector <pair<int,int>> a_of_v[n];   

动态向量数组可以实现极低的访问延迟，并且有很低的存储空间浪费，但是却并不能解决另外的几个问题：

• 并发访问支持
• 数据删除时的额外代价（例如存储空白空间回填等）

在工业界中，典型的高性能哈希表的实现有例如谷歌的 SparseHash 库，它实现了一种叫做 dense_hash_map 的哈希表。在 C++ 标准 11 中实现了 unordered_map，是一种锁链式的哈希表，它通过牺牲一定的存储空间来获取快速寻址性能。但是以上两种实现的问题是，他们都没有和底层的硬件（CPU 内核）并发算力同步的扩张能力，换句话说是一种单线程哈希表实现，任何时刻只有单读或单写进程占据全部的表资源——这或许可以算作是对底层资源的一种浪费吧。

在高性能云计算环境下，通过并发计算可以获得更高的系统吞吐率，通常这也意味着底层的数据结构是支持并发的（concurrent data structure），并且能利用多核 CPU、每核多线程，并能利用多机（无论是物理上还是逻辑上的）协同并发的针对一个逻辑上的大数据集进行并发处理。

传统的哈希实现几乎都是单线程、单任务的，意味着它们采用的是阻塞式设计，第二个线程或任务如果试图访问同一个资源池，它会被阻塞而等待，以至于无法（实时）完成任务。

从上面的单写单读向前进化，很自然的一个小目标是单写多读，我们称之为 single-writer-multiple-reader 的并发哈希，它允许多个读线程去访问同一个资源池里的关键区域（critical section）。当然，这种设计中只允许任何时刻最多存在一个写的线程。

单写多读的设计实现中通常会使用一些技术手段，例如：

• Versioning：中文称为版本号记录
• RCU (Read-Copy-Update)：中文称为读-拷贝-更新
• Open-Addressing：中文称为开放式寻址

以 RCU 为例，Linux 操作系统的内核中首先使用了这种技术来支持多读。在 MemC3/Cuckoo 哈希实现中则使用了开放寻址技术，如图 Diagram-3 所示。

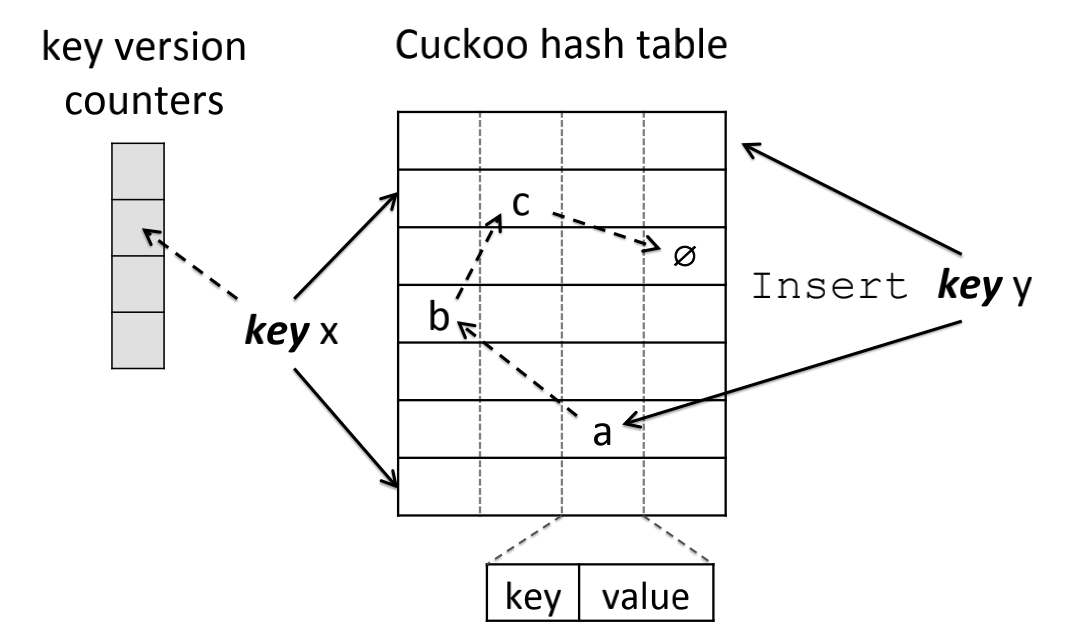
Diagram-3：Cuckoo 哈希的键被映射到了 2 个桶中以及使用了 1 个版本计数器

沿着上面的思路继续向前迭代，我们当然希望可以实现多读多写的真正意义上的高并发数据结构。但是，这个愿景似乎与 ACID（数据强一致性）的要求相违背—在商用场景中，多个任务或线程在同一时间对同一个数据进行写、读等操作而可能造成的数据不一致而导致的混乱的问题。下面我们来把以上的挑战和问题细化后逐一解决。

实现可扩展的高并发哈希数据结构需要克服我们在上面提到的几个主要问题：

• 无阻塞或无锁式设计（Non-blocking and Lock-Free）
• 精细颗粒度的访问控制（Fine-granularity Access Control）

要突破并实现上面提到的两条，两者都和并发访问控制高度相关，有如下的要点需要考量：

• 核心区域（访问控制）：
  • 区域足够小
  • 执行时间足够短
• 通用数据访问：
  • 避免不必要的访问（Unnecessary）
  • 避免无意识的访问（Unintentional）
• 并发控制：
  • 使用精细颗粒度的锁实现，例如 lock-striping（条纹锁）
  • 采用推测式上锁机制，例如交易过程中的合并锁机制（Transactional Lock Elision）

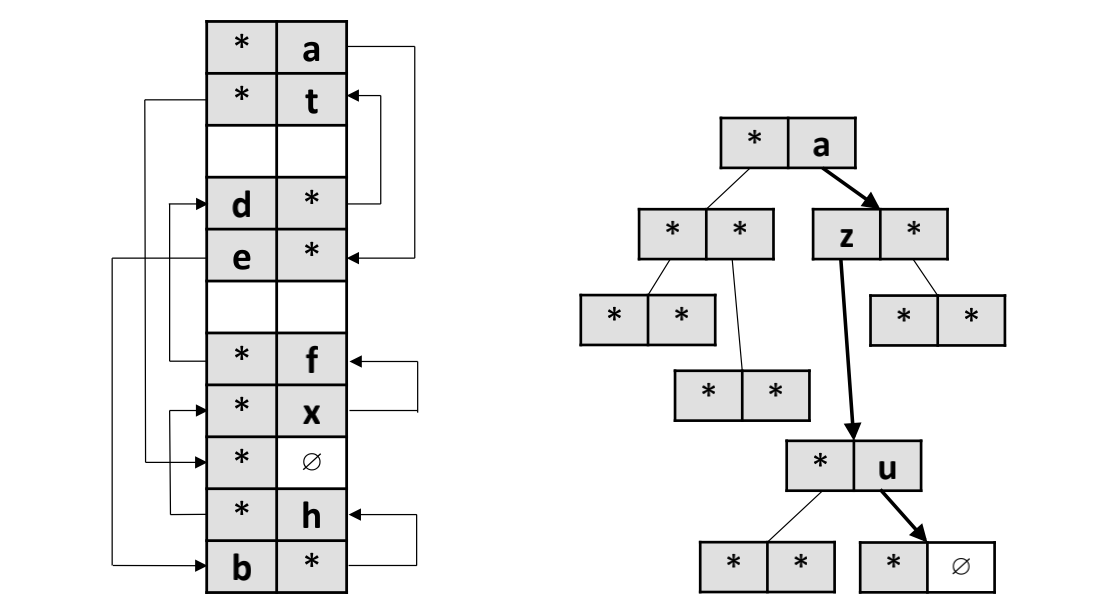
Diagram-4: 随机放置vs.基于BFS的双向集合关联式哈希

对于一个高并发系统而言，它通常会至少包含如下三套机制协同工作才能实现充分的并发：

• 并发的基础架构
• 并发的数据结构
• 并发的算法实现

以上三者，在图数据库、图计算与存储引擎系统的设计中更是缺一不可。

并发的基础架构包含有硬件和软件的基础架构，例如英特尔的中央处理器的 TSX (Transactional Synchronization Extensions，交易同步扩展）功能是硬件级别的在英特尔 64 位架构之上的交易型内存支持。在软件层面，应用程序可以把一段代码声明为一笔交易，而在这段代码执行期间的操作为原子操作。像 TSX 这样的功能可以实现平均达到 140% 的性能加速。这也是 Intel 推出的相对于其它 X86 架构处理器的一种竞争优势。当然这种硬件功能对于代码而言不完全是透明的，它在一定程度上也增加了编程的复杂度和程序的跨平台迁移复杂度。

在软件层面，更多的考量是操作系统本身对于高并发的支持，通常我们认为 Linux 操作系统在内核到库级别对于并发的支持要好于 Windows 操作系统，尽管这个并不绝对，甚至是很多的底层实现，例如虚拟化、容器等的实现让上层的应用程序对于底层的直接依赖性得以降低。 

另一方面，有了并发的数据结构，在代码编程层面，你依然需要设计代码逻辑、算法逻辑来充分的利用和释放并发的数据处理能力。特别是对于图数据集和图数据结构而言，并发对于程序员而言是一种思路的转变，充分的利用并发的能力，你可能可以获得成百上千倍的性能提升，在同样的硬件资源基础上，在同样的数据结构基础上，在同样的编程语言实现上，永远不要忽略并发实现的意义和价值。

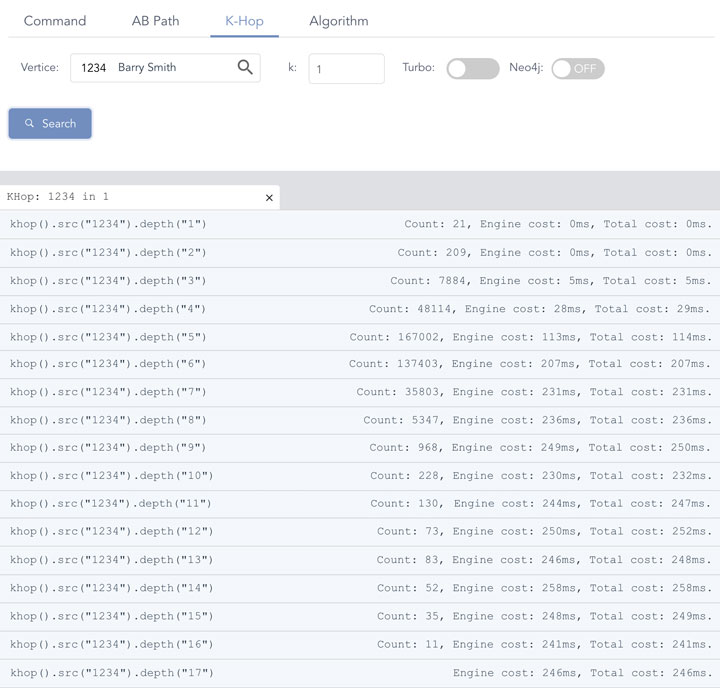
Diagram-5：嬴图的基于高并发哈希实现的实时深度图遍历

上图（Diagram-5）当中展示了在嬴图之上，一款高性能、高并发实时图数据库服务器，通过高并发架构、数据结构以及图算法实现的高性能K邻操作的性能。

K邻（英文 K-Hop）操作通常是通过 BFS（广度优先搜索）的方式实现的。图中的测试数据和结果是在一个常见的用于性能评测的图数据集上（例如 Amazon 0601 数据集，有 340 万条边和 41 万顶点）实现的，从任一顶点出发计算与它的最短距离为 K 步的邻居的数量（和邻居集合），直到找完图中最深的邻居后没有新邻居发现后返回。

注：在商用场景中图的大小通常在百万、千万、亿甚至十亿以上的数量级，而学术界中用于发论文的图数据集的数量级则经常在千、万的数量级，两者之间存在着由量变到引发质变的区别——特别对于算法复杂度和数据结构的并发驾驭能力而言，读者需要对此注意区分和甄别。以 Dijkstra’s 最短路径算法为例，它的原生算法完全是串行的，在小图当中或许还可以通过对全图进行全量计算来实现，在大图之上则完全不具有可行性！

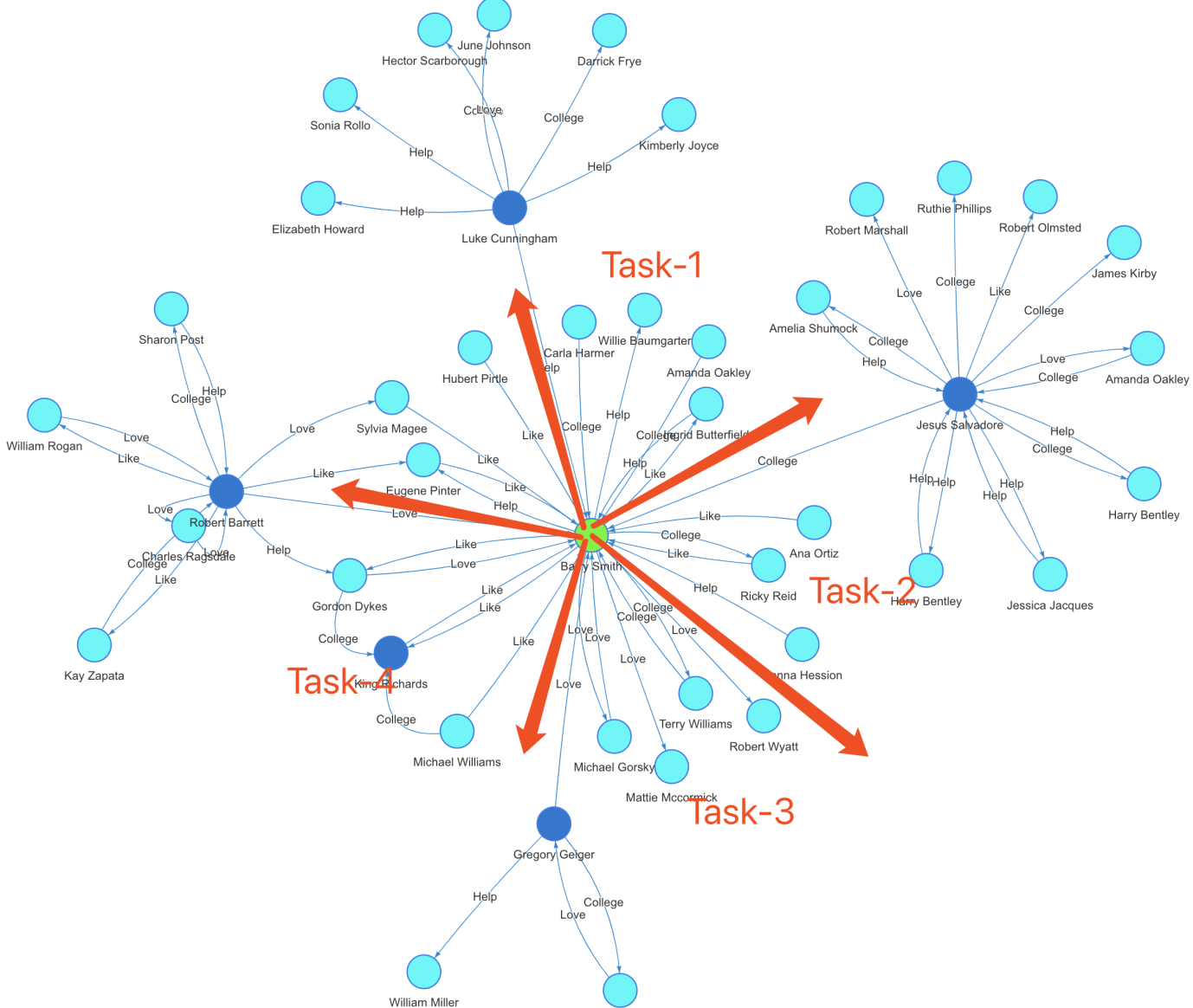
Diagram-6：K邻并发算法

BFS 是相对于 DFS（深度优先搜索）或其它图上算法（例如鲁汶社区识别等）而言比较容易实现并发计算的，上图（Diagram-6）中形象的解析了如何在图中实现 BFS 算法并发。我们以 BFS 为例为读者解读如何实现高并发。

K邻并发算法步骤如下：

1. 在图中定位起始顶点（上图中的绿色顶点），计算其直接关联的具有唯一性的邻居数量。如果 K=1，直接返回邻居数量；否则，执行下一步。
2. K>=2, 确定参与并发计算的资源量，并根据第一步中返回的邻居数量决定每个并发线程（任务）所需处理的任务量大小，进入第三步。
3. 每个任务进一步以分而治之的方式，计算当前面对的（被分配）顶点的邻居数量，以递归的方式前进，直到满足深度为K或者无新的邻居顶点可以被返回而退出，结束。

基于以上的算法描述，我们再来回顾一下 Diagram-5 中的实现效果，当K邻计算深度为 1-2 层的时候，内存计算引擎在微秒级内完成计算。从第 3 跳开始，返回的邻居数量呈现指数级快速上涨（2-Hop 邻居 ~200，3-Hop 邻居 ~8000，4-Hop 邻居接近 5 万）的趋势，这就意味着计算复杂度也等比上涨。但是，通过饱满的并发操作，系统的延时保持在了相对低的水平，并呈现了线性甚至亚线性的增长趋势（而不是指数级增长趋势！），特别是在搜索深度第 6 层到第 17 层的区间内，系统时延几乎稳定在 ~200ms 的范围！

注：第 17 层（17-Hop）返回的邻居数量为 0，因为此时全图（联通子图）已经遍历完毕，没有找到任何深度达到 17 层的顶点邻居，因此返回结果集合大小为 0。

如果我们做一个 1 比 1 的对标，同样的数据集，在同样的硬件配置的公有云服务器上用 Neo4j 来做同样的K邻操作，效果如下：

• 1-Hop：~200毫秒，比嬴图慢了 1,000倍！
• 从 5-Hop 开始，几乎无法实时返回（系统内存资源耗尽前未能返回结果）
• K邻的结果默认情况下没有去重。有大量重复邻居顶点在结果集中。
• 随着搜索深度的增加，返回时间和系统消耗呈现指数级（超线性）增长趋势。
• 最大并发为 400%（4 线程并发），远低于嬴图的 6400% 并发规模。

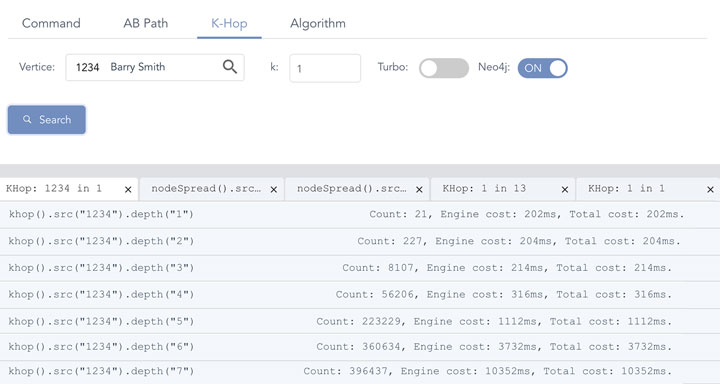
Diagram-7：Neo4j 数据库的图遍历性能

基于 Neo4j 的实验，我们只进行到 7-Hop 后就不得不终止了，因为 7 跳的时候系统耗时超过 10 秒钟，从 8 跳开始 Neo4J 几乎不可能返回结果。而最大的问题是计算结果并不正确，这种不正确包含两个维度：

• 重复顶点未被去重
• 顶点深度计算错误

K-hop 中返回的应该是最短路径条件下的邻居，那么如果第一层的直接邻居中已经被返回的顶点，不可能也不应该出现在第二层或第三层或其它层级的邻居列表中！很明显 Neo4J，还有其它一些图数据库（例如腾讯的星图）在 K-hop 的实现中没有遵循 BFS 的原则（或者是实现算法错误），也没有实现去重，甚至没有办法返回（任意深度）全部的邻居。

注：在更大的数据集中，例如 Twitter 的 15 亿条边、4200 万顶点、26GB 大小的社交数据集中，K-hop 的操作的挑战更加巨大，我们已知的很多图数据库都无法在其上完成深度（>=3）的 K-hop 查询，例如 Neo4J、JanusGraph、Titan、亚马逊的Neptune、ArangoDB、百度的 HugeGraph 等。而在能完成的为数不多的几个图数据库中，嬴图也指数级快于其它玩家。具体指标参考下图。

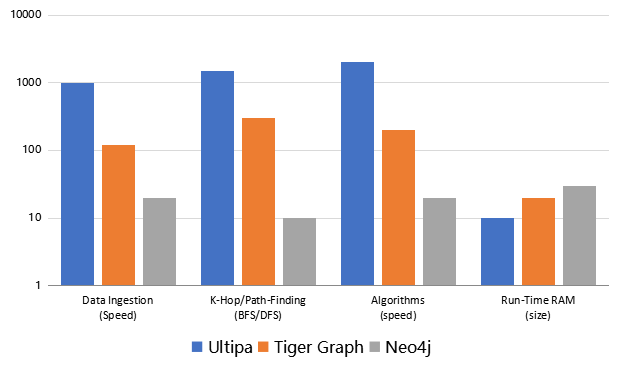
Diagram-8：性能评测对标 - 嬴图 vs. Neo4J vs. Tiger Graph

如果读者对于本文中提及的嬴图的实现中所用到的 Adjacency Hash<*> 数据结构的设计与实现的细节感兴趣，可以在国家知识产权局的数据库中查询嬴图团队提交的相关专利（专利号2020****5644）或联系我们索取。

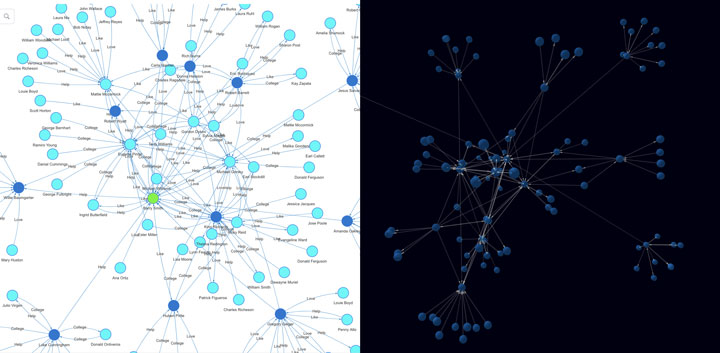
Diagram-9：嬴图的二维和三维可视化

值得补充一点的是，尽管性能对于图数据库、图计算而言甚为重要，可视化功能也不可忽略。因为相比于传统的关系型数据库的二维表中的行 vs. 列的结构，图是高维度的、更直观的、可解释的，图中的运算结果的可视化是非常必要、甚至是必须的。这也是为什么我们提出了一个观点：白盒化 AI、可解释 AI需要通过知识图谱 + 图数据库来实现，前者本质上就是交互可视化，而它基于的是后者的算力突破！上图中展示的是 嬴图Manager（嬴图数据库集成的可视化前端操作界面&图数据库、图谱管理平台）中的对图上实时计算的 2D 和 3D 可视化效果。

到这里，我们来总结一下图数据结构的演化：更高的吞吐率可以通过更高的并发来实现，而这可以贯穿整个数据的全生命周期：

• 数据导入、加载（Data Ingestion）
• 数据转换（Data Transformation）
• 数据计算（无论是K邻还是路径还是…）
• 基于批处理的操作、图算法等

另外，内存消耗也是一个不可忽略的存储要素，尽管我们这几年都纷纷开始宣称内存就是新的硬盘，它的性能指数级高于固态硬盘或磁盘，但是，它并不是没有成本的，因此审慎的内存使用是必要的，例如以下的降低内存消耗的策略：

• 基于数据加速的数据建模（Data Modeling for Data Acceleration）
• 数据压缩与数据去重（Data Compression & De-duplication）
• 算法实现与代码编程中避免过多的数据膨胀、数据拷贝等操作

希望读者能从本文中获取一些有用的信息，那么我们最早决定写这篇文章的目的就已经达到了。另外，我们克制了在文章中加入大量数学公式的冲动，目的只是为了让你可以不必牺牲大量脑细胞的条件下读懂本文。毕竟，数据结构和软件工程不是博士们的专利。