概述
二分图(Bipartite Graph)算法用于确定给定的图是否为二分图。通过应用该算法,可以在不同情况下识别和利用二分图的固有结构,实现有效的资源分配、任务分配和分组优化。
如果一个图为二分图,本算法返回1,否则返回0。
基本概念
二分图
二分图中的节点可以划分至两个不相交的集合,且图中的每条边都连接一个集合中的节点和另一个集合中的节点。换句话说,不存在连接同一集合内节点的边。

这是一个示例的二分图,它的节点可以划分至集合V1 = {A, D, E}和V2 = {B, C, F}。
着色法
要确定一个图是否为二分图,一种常见的方法是进行图遍历并将每个访问的节点分配到两个不同的集合中。这个过程通常被称为对节点进行"着色"。在遍历过程中,如果遇到连接两个同一集合中的节点的边,则该图不是二分图。相反,如果所有的边连接来自不同集合的节点,那么该图是二分图。
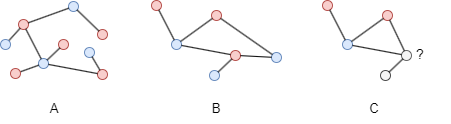
在这个例子中,图A和图B都是二分图。图C不是二分图,因为它包含一个奇数环。奇数环(Odd Cycle)是指节点数为奇数的环路。二分图不能包含奇数环,因为无法使用两种颜色对奇数环中的所有节点进行着色,同时满足二分图的要求。这种特性,即二分图不包含任何奇数环,是二分图的基本特征之一。
特殊说明
- 自环边的两个端点是同一个节点,因此含有自环边的图都不是二分图。
- 二分图算法忽略边的方向,按照无向边进行计算。
示例图
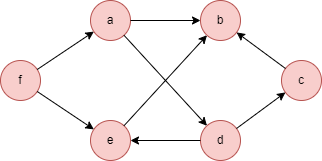
在一个空图中运行以下语句定义图结构并插入数据:
INSERT (a:default {_id: "a"}),
(b:default {_id: "b"}),
(c:default {_id: "c"}),
(d:default {_id: "d"}),
(e:default {_id: "e"}),
(f:default {_id: "f"}),
(a)-[:default]->(b),
(a)-[:default]->(d),
(c)-[:default]->(b),
(d)-[:default]->(c),
(d)-[:default]->(e),
(e)-[:default]->(b),
(f)-[:default]->(a),
(f)-[:default]->(e);
insert().into(@default).nodes([{_id:"a"}, {_id:"b"}, {_id:"c"}, {_id:"d"}, {_id:"e"}, {_id:"f"}]);
insert().into(@default).edges([{_from:"a", _to:"b"}, {_from:"a", _to:"d"}, {_from:"c", _to:"b"}, {_from:"d", _to:"c"}, {_from:"d", _to:"e"}, {_from:"e", _to:"b"}, {_from:"f", _to:"a"}, {_from:"f", _to:"e"}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:bipartite
该算法不需要任何参数。
文件回写
CALL algo.bipartite.write("my_hdc_graph", {},
{
file: {
filename: "isBipartite"
}
})
algo(bipartite).params({
projection: "my_hdc_graph"
}).write({
file: {
filename: "isBipartite"
}
})
bipartite_result: 1
统计回写
CALL algo.bipartite.write("my_hdc_graph", {},
{
stats: {}
})
exec{
algo(bipartite).params().stream() as result
return result
} on my_hdc_graph
结果:
| bipartite_result |
|---|
| true |
完整返回
CALL algo.bipartite.run("my_hdc_graph") YIELD r
RETURN r
exec{
algo(bipartite).params() as r
return r
} on my_hdc_graph
结果:
| bipartite_result |
|---|
| 1 |
流式返回
CALL algo.bipartite.stream("my_hdc_graph") YIELD r
RETURN r
exec{
algo(bipartite).params().stream() as r
return r
} on my_hdc_graph
结果:
| bipartite_result |
|---|
| 1 |
统计返回
CALL algo.bipartite.stats("my_hdc_graph") YIELD r
RETURN r
exec{
algo(bipartite).params().stats() as result
return result
} on my_hdc_graph
结果:
| bipartite_result |
|---|
| 1 |
