概述
局部聚类系数(Local Clustering Coefficient)算法计算节点邻居之间连接的密度。它量化了邻居之间实际连接与可能连接之间的比值。
局部聚类系数体现了节点自我网络(Ego Network)的凝聚性。在社交网络中,局部聚类系数能够帮助理解一个人认识的人之间的相互连接程度。较高的局部聚类系数意味着他认识的人很可能也相互认识,这表明存在一个紧密结合的社交群体,例如家庭。相反,较低的局部聚类系数表示自我网络的连接较松散,他认识的人之间没有紧密的连接。
基本概念
局部聚类系数
在数学上,无向图中节点的局部聚类系数是相连的邻居节点对数量与所有可能的邻居节点对数量的比值:
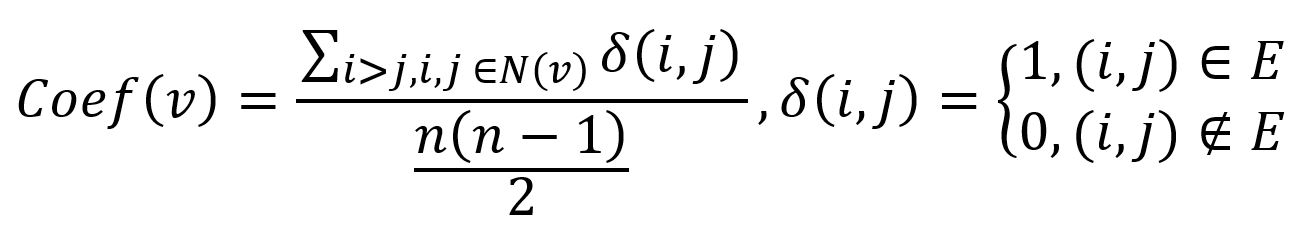
其中,n表示节点v的一步邻域(表示为 N(v))节点数,i和j是N(v)中的任意两个不同的节点,如果i和j有边相连,δ(i,j)等于1,否则为0。
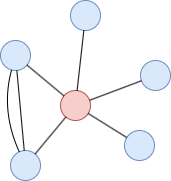
本例中,红色节点的局部聚类系数为1/(5*4/2) = 0.1。
特殊说明
- 局部聚类系数算法忽略边的方向,按照无向边进行计算。
示例图
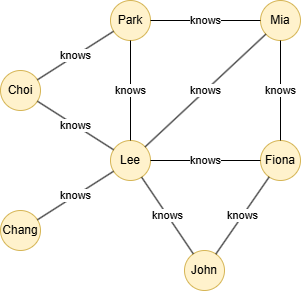
在一个空图中运行以下语句定义图结构并插入数据:
ALTER GRAPH CURRENT_GRAPH ADD EDGE {
knows ()-[]->()
};
INSERT (Lee:default {_id: "Lee"}),
(Choi:default {_id: "Choi"}),
(Mia:default {_id: "Mia"}),
(Fiona:default {_id: "Fiona"}),
(Chang:default {_id: "Chang"}),
(John:default {_id: "John"}),
(Park:default {_id: "Park"}),
(Choi)-[:knows]->(Park),
(Choi)-[:knows]->(Lee),
(Park)-[:knows]->(Lee),
(Park)-[:knows]->(Mia),
(Lee)-[:knows]->(Mia),
(Mia)-[:knows]->(Fiona),
(Fiona)-[:knows]->(Lee),
(Lee)-[:knows]->(Chang),
(Lee)-[:knows]->(John),
(John)-[:knows]->(Fiona);
create().edge_schema("knows");
insert().into(@default).nodes([{_id:"Lee"}, {_id:"Choi"}, {_id:"Mia"}, {_id:"Fiona"}, {_id:"Chang"}, {_id:"John"}, {_id:"Park"}]);
insert().into(@knows).edges([{_from:"Choi", _to:"Park"}, {_from:"Choi", _to:"Lee"}, {_from:"Park", _to:"Lee"}, {_from:"Park", _to:"Mia"}, {_from:"Lee", _to:"Mia"}, {_from:"Mia", _to:"Fiona"}, {_from:"Fiona", _to:"Lee"}, {_from:"Lee", _to:"Chang"}, {_from:"Lee", _to:"John"}, {_from:"John", _to:"Fiona"}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:clustering_coefficient
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
ids |
[]_id |
/ | / | 是 | 通过_id指定参与计算的点;若未设置则计算所有点 |
uuids |
[]_uuid |
/ | / | 是 | 通过_uuid指定参与计算的点;若未设置则计算所有点 |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点 |
limit |
Integer | ≥-1 | -1 |
是 | 限制返回的结果数;-1返回所有结果 |
order |
String | asc, desc |
/ | 是 | 根据局部聚类系数clce_centrality对结果排序 |
文件回写
CALL algo.clustering_coefficient.write("my_hdc_graph", {
ids: ["Lee", "Choi"],
return_id_uuid: "id"
}, {
file: {
filename: "lcc"
}
})
algo(clustering_coefficient).params({
projection: "my_hdc_graph",
ids: ["Lee", "Choi"],
return_id_uuid: "id"
}).write({
file: {
filename: "lcc"
}
})
结果:
_id,clce_centrality
Lee,0.266667
Choi,1
数据库回写
将结果中的clce_centrality值写入指定点属性。该属性类型为float。
CALL algo.clustering_coefficient.write("my_hdc_graph", {}, {
db: {
property: "lcc"
}
})
algo(clustering_coefficient).params({
projection: "my_hdc_graph"
}).write({
db: {
property: "lcc"
}
})
完整返回
CALL algo.clustering_coefficient.run("my_hdc_graph", {
return_id_uuid: "id",
order: "desc"
}) YIELD r
RETURN r
exec{
algo(clustering_coefficient).params({
return_id_uuid: "id",
order: "desc"
}) as result
return result
} on my_hdc_graph
结果:
| _id | clce_centrality |
|---|---|
| John | 1 |
| Choi | 1 |
| Park | 0.666667 |
| Fiona | 0.666667 |
| Mia | 0.666667 |
| Lee | 0.266667 |
| Chang | 0 |
流式返回
CALL algo.clustering_coefficient.stream("my_hdc_graph", {}) YIELD r
FILTER r.clce_centrality = 1
RETURN count(r)
exec{
algo(clustering_coefficient).params().stream() as r
where r.clce_centrality == 1
return count(r)
} on my_hdc_graph
结果:2
