概述
单源最短路径问题(Single-Source Shortest Path, SSSP)计算的是从图中一个源节点到其余所有可达节点的最短路径。最短路径是指全部可能的路径中,所有边的权重和最小的路径;在无权图的情况下,是指边的数量最少的路径。最短路径的成本(或距离)是指所有边的权重和或数量。
Dijkstra(迪杰斯特拉)算法最初是由荷兰计算机科学家Edsger W. Dijkstra在1956年构思的,用于找到两个给定节点间的最短路径。单源最短路径是一种常见的变种,有助于进行有效的路径规划和网络分析。
基本概念
Dijkstra单源最短路径
我们将通过计算示例图中以b为源节点的无向加权最短路径来解释Dijkstra单源最短路径算法的基本实现:
1. 创建一个优先队列来存储节点及其与源节点之间的距离。初始化源节点的距离为0,其余节点为无穷大。所有节点标记为未访问。

2. 从队列中提取距离最小的节点,将其标记为已访问,对该节点的所有“未访问”邻居进行松弛操作。

dist(a) = min(0+2,∞) = 2, dist(c) = min(0+1,∞) = 1
松弛操作是指通过考虑经过节点u的路径,更新与节点u相连的节点v的距离,使其获得可能的更短距离。具体来说,节点v的距离会被更新为dist(v) = dist(u) + w(u,v),其中w(u,v)是边(u,v)的权重。此更新仅在当前dist(v)大于dist(u) + w(u,v)时进行。
一旦节点被标记为已访问,其最短路径就被确定了,其距离在算法的余下过程中将不再改变。算法仅更新尚未访问过的节点的距离。
3. 重复步骤2,直到所有节点都被访问过。

dist(d) = min(1+3, ∞) = 4, dist(e) = min(1+4, ∞) = 5, dist(g) = min(1+2, ∞) = 3

dist(d) = min(2+4, 4) = 4

dist(f) = min(3+5, ∞) = 8

No neighbor can be relaxed

dist(f) = min(5+8, 8) = 8

没有邻居可以被松弛
所有节点都访问过了,算法结束
特殊说明
- Dijkstra算法适用于具有非负边权重的图。如果存在负权重,Dijkstra算法输出的结果也许是不正确的。这种情况建议使用 SPFA算法。
- 如果两个节点之间存在多条最短路径,算法会找出所有这些路径。
- 在非连通图中,算法只输出源节点所在的连通分量内所有节点到源节点的最短距离。
示例图
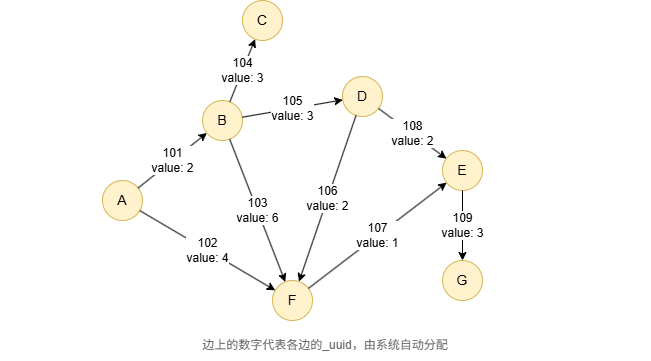
在一个空图中运行以下语句定义图结构并插入数据:
ALTER EDGE default ADD PROPERTY {
value int32
};
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(A)-[:default {value: 2}]->(B),
(A)-[:default {value: 4}]->(F),
(B)-[:default {value: 3}]->(C),
(B)-[:default {value: 3}]->(D),
(B)-[:default {value: 6}]->(F),
(D)-[:default {value: 2}]->(E),
(D)-[:default {value: 2}]->(F),
(E)-[:default {value: 3}]->(G),
(F)-[:default {value: 1}]->(E);
create().edge_property(@default, "value", int32);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}]);
insert().into(@default).edges([{_from:"A", _to:"B", value:2}, {_from:"A", _to:"F", value:4}, {_from:"B", _to:"F", value:6}, {_from:"B", _to:"C", value:3}, {_from:"B", _to:"D", value:3}, {_from:"D", _to:"F", value:2}, {_from:"F", _to:"E", value:1}, {_from:"D", _to:"E", value:2}, {_from:"E", _to:"G", value:3}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:sssp
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
ids |
_id |
/ | / | 否 | 通过_id指定单个源节点 |
uuids |
_uuid |
/ | / | 否 | 通过_uuid指定单个源节点 |
direction |
String | in, out |
/ | 是 | 指定最短路径中所有边的方向,in表示仅包含入边,out表示仅包含出边;若未设置则不考虑边方向 |
edge_schema_property |
[]"<@schema.?><property>" |
/ | / | 是 | 作为权重的数值类型边属性,权重值为所有指定属性值的总和;不包含指定属性的边将被忽略 |
record_path |
Integer | 0, 1 |
0 |
是 | 是否在结果中包含最短路径。设定为1时,返回totalCost和最短路径;设置为0时,仅返回totalCost |
impl_type |
String | dijkstra |
beta |
否 | 指定SSSP算法的执行类型;计算Dijkstra单源最短路径时,设置为dijkstra;beta是嬴图默认最短路径算法 |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点。仅可使用_uuid表示边 |
limit |
Integer | ≥-1 | -1 |
是 | 限制返回的结果数;-1返回所有结果 |
order |
String | asc, desc |
/ | 是 | 根据totalCost值对结果排序 |
文件回写
CALL algo.sssp.write("my_hdc_graph", {
ids: "A",
edge_schema_property: "@default.value",
impl_type: "dijkstra",
return_id_uuid: "id"
}, {
file: {
filename: "costs"
}
})
algo(sssp).params({
projection: "my_hdc_graph",
ids: "A",
edge_schema_property: "@default.value",
impl_type: "dijkstra",
return_id_uuid: "id"
}).write({
file: {
filename: "costs"
}
})
结果:
_id,totalCost
D,5
F,4
B,2
E,5
C,5
G,8
CALL algo.sssp.write("my_hdc_graph", {
ids: "A",
edge_schema_property: "@default.value",
impl_type: "dijkstra",
record_path: 1,
return_id_uuid: "id"
}, {
file: {
filename: "paths"
}
})
algo(sssp).params({
projection: "my_hdc_graph",
ids: "A",
edge_schema_property: "@default.value",
impl_type: "dijkstra",
record_path: 1,
return_id_uuid: "id"
}).write({
file: {
filename: "paths"
}
})
结果:
totalCost,_ids
8,A--[102]--F--[107]--E--[109]--G
5,A--[101]--B--[105]--D
5,A--[102]--F--[107]--E
5,A--[101]--B--[104]--C
4,A--[102]--F
2,A--[101]--B
完整返回
CALL algo.sssp.run("my_hdc_graph", {
ids: 'A',
edge_schema_property: 'value',
impl_type: 'dijkstra',
record_path: 0,
return_id_uuid: 'id',
order: 'desc'
}) YIELD r
RETURN r
exec{
algo(sssp).params({
ids: 'A',
edge_schema_property: 'value',
impl_type: 'dijkstra',
record_path: 0,
return_id_uuid: 'id',
order: 'desc'
}) as r
return r
} on my_hdc_graph
结果:
| _id | totalCost |
|---|---|
| G | 8 |
| D | 5 |
| E | 5 |
| C | 5 |
| F | 4 |
| B | 2 |
流式返回
CALL algo.sssp.stream("my_hdc_graph", {
ids: 'A',
edge_schema_property: '@default.value',
impl_type: 'dijkstra',
record_path: 1,
return_id_uuid: 'id'
}) YIELD r
RETURN r
exec{
algo(sssp).params({
ids: 'A',
edge_schema_property: '@default.value',
impl_type: 'dijkstra',
record_path: 1,
return_id_uuid: 'id'
}).stream() as r
return r
} on my_hdc_graph
结果:
totalCost |
_ids |
|---|---|
| 8 | ["A","102","F","107","E","109","G"] |
| 5 | ["A","101","B","105","D"] |
| 5 | ["A","102","F","107","E"] |
| 5 | ["A","101","B","104","C"] |
| 4 | ["A","102","F"] |
| 2 | ["A","101","B"] |
