概述
特征向量中心性(Eigenvector Centrality)度量图中点的影响力。一个点的影响力取决于它的邻居,即受到邻居的影响,也能够影响邻居。值得注意的是,邻居点的影响力各不相同,邻居越有影响力,该点的影响力也越大。
特征向量中心性的取值范围是0到1,值越大,影响力越大。
基本概念
特征向量中心性
点的影响力通过递归的方式计算。以下图为例,假定点通过入边接收邻居的影响,邻接矩阵A的元素Aij反映点i的入边数量。随机初始化所有点的中心性值——以全部是1为例——并用向量c(0)表示。

在每轮影响力传递中,每个点的中心性更新为其入边邻居的中心性之和。在第一轮,此操作相当于将向量c(0)与邻接矩阵A相乘,即c(1) = Ac(0)。接着,使用L2范数将该向量c(1)进行归一化处理:

经过k轮传递,向量c(k)可通过c(k) = Ac(k-1)计算。随着k增长,c(k)趋于稳定。本例中,c(k)在约20轮后不再改变,c(k)各元素值即为对应点的中心性值。
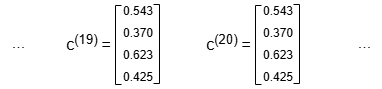
算法在c(k)所有元素的变化值之和小于规定的收敛偏差时,或迭代轮数达到限制时结束。
特征值和特征向量
给定nxn维矩阵A、常数λ以及n维非0向量x,如果满足Ax = λx,那么称λ为A的特征值(Eigenvalue),x为A对应该特征值的特征向量(Eigenvector)。
上面的邻接矩阵A有四个特征值λ1、λ2、λ3和λ4,分别对应特征向量x1、x2、x3和x4。其中,x1是对应于绝对值最大的特征值λ1的特征向量,λ1称为主特征值,x1称为主特征向量。
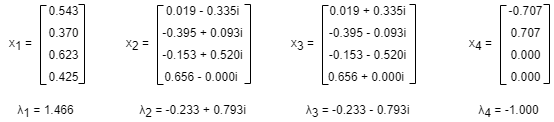
事实上,无论c(0)初始值是多少,随着k增大,c(k)总是朝着x1的方向收敛。这一点可由Perron-Forbenius定理证实。因此,计算图中各点的特征向量中心性就是计算图的邻接矩阵A的主特征向量。
特殊说明
- 为解决无环有向图的影响力泄露问题,本算法使用邻接矩阵加上单位矩阵后的矩阵(即
A = A + I)而非邻接矩阵本身来进行计算。 - 自环边被视为一条入边和一条出边。
示例图
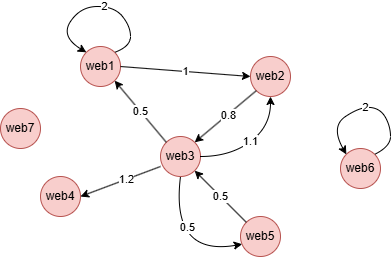
在一个空图中运行以下语句定义图结构并插入数据:
ALTER GRAPH CURRENT_GRAPH ADD NODE {
web ()
};
ALTER GRAPH CURRENT_GRAPH ADD EDGE {
link ()-[{value float}]->()
};
INSERT (web1:web {_id: "web1"}),
(web2:web {_id: "web2"}),
(web3:web {_id: "web3"}),
(web4:web {_id: "web4"}),
(web5:web {_id: "web5"}),
(web6:web {_id: "web6"}),
(web7:web {_id: "web7"}),
(web1)-[:link {value: 2}]->(web1),
(web1)-[:link {value: 1}]->(web2),
(web2)-[:link {value: 0.8}]->(web3),
(web3)-[:link {value: 0.5}]->(web1),
(web3)-[:link {value: 1.1}]->(web2),
(web3)-[:link {value: 1.2}]->(web4),
(web3)-[:link {value: 0.5}]->(web5),
(web5)-[:link {value: 0.5}]->(web3),
(web6)-[:link {value: 2}]->(web6);
create().node_schema("web").edge_schema("link");
create().edge_property(@link, "value", float);
insert().into(@web).nodes([{_id:"web1"}, {_id:"web2"}, {_id:"web3"}, {_id:"web4"}, {_id:"web5"}, {_id:"web6"}, {_id:"web7"}]);
insert().into(@link).edges([{_from:"web1", _to:"web1",value:2}, {_from:"web1", _to:"web2",value:1}, {_from:"web2", _to:"web3",value:0.8}, {_from:"web3", _to:"web1",value:0.5}, {_from:"web3", _to:"web2",value:1.1}, {_from:"web3", _to:"web4",value:1.2}, {_from:"web3", _to:"web5",value:0.5}, {_from:"web5", _to:"web3",value:0.5}, {_from:"web6", _to:"web6",value:2}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:eigenvector_centrality
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
max_loop_num |
Integer | ≥1 | 20 |
是 | 最大迭代轮数。算法将在完成所有轮次后停止 |
tolerance |
Float | (0,1) | 0.001 |
是 | 某轮迭代后,若所有点的分值变化小于指定tolerance时,表明结果已稳定,算法会停止 |
edge_weight_property |
"<@schema.?><property>" |
/ | / | 是 | 邻接矩阵A中用作权重的数值类型边属性;不包含指定属性的边将被忽略 |
direction |
String | in, out |
/ | 是 | 使用点的入边(in)或出边(out)构建邻接矩阵A |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点 |
limit |
Integer | ≥-1 | -1 |
是 | 限制返回的结果数;-1返回所有结果 |
order |
String | asc, desc |
/ | 是 | 根据eigenvector_centrality分值对结果排序 |
文件回写
CALL algo.eigenvector_centrality.write("my_hdc_graph", {
return_id_uuid: "id",
max_loop_num: 50,
tolerance: 0.000001,
direction: "in",
order: "desc"
}, {
file: {
filename: "eigenvector_centrality"
}
})
algo(eigenvector_centrality).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
max_loop_num: 50,
tolerance: 0.000001,
direction: "in",
order: "desc"
}).write({
file: {
filename: "eigenvector_centrality"
}
})
结果:
_id,eigenvector_centrality
web1,0.573612
web2,0.573612
web3,0.460001
web5,0.255281
web4,0.255281
web6,1.35778e-05
web7,6.32265e-15
数据库回写
将结果中的eigenvector_centrality值写入指定点属性。该属性类型为double。
CALL algo.eigenvector_centrality.write("my_hdc_graph", {
edge_weight_property: "@link.value"
}, {
db: {
property: "ec"
}
})
algo(eigenvector_centrality).params({
projection: "my_hdc_graph",
edge_weight_property: "@link.value"
}).write({
db:{
property: 'ec'
}
})
完整返回
CALL algo.eigenvector_centrality.run("my_hdc_graph", {
return_id_uuid: "id",
max_loop_num: 300,
tolerance: 0.000001,
edge_weight_property: "value",
direction: "in",
order: "desc"
}) YIELD ec
RETURN ec
exec{
algo(eigenvector_centrality).params({
return_id_uuid: "id",
max_loop_num: 300,
tolerance: 0.000001,
edge_weight_property: "value",
direction: "in",
order: "desc"
}) as ec
return ec
} on my_hdc_graph
结果:
| _id | eigenvector_centrality |
|---|---|
| web1 | 0.835474799052068 |
| web2 | 0.497522870627321 |
| web3 | 0.198903901628052 |
| web4 | 0.112638313459419 |
| web5 | 0.046932628743156 |
| web6 | 0.000173115768280974 |
| web7 | 3.67918716589409e-105 |
流式返回
CALL algo.eigenvector_centrality.stream("my_hdc_graph", {
return_id_uuid: "id",
max_loop_num: 300,
tolerance: 0.000001,
edge_weight_property: "value",
direction: "in",
order: "desc"
}) YIELD ec
RETURN ec
exec{
algo(eigenvector_centrality).params({
return_id_uuid: "id",
max_loop_num: 300,
tolerance: 0.000001,
edge_weight_property: "value",
direction: "in",
order: "desc"
}).stream() as ec
return ec
} on my_hdc_graph
结果:
| _id | eigenvector_centrality |
|---|---|
| web1 | 0.835474799052068 |
| web2 | 0.497522870627321 |
| web3 | 0.198903901628052 |
| web4 | 0.112638313459419 |
| web5 | 0.046932628743156 |
| web6 | 0.000173115768280974 |
| web7 | 3.67918716589409e-105 |
