概述
HyperANF(Hyper-Approximate Neighborhood Function,超近似邻域函数)算法用于估算图平均距离。它在准确性和计算效率之间取得了平衡,适用于大型图,精确计算大型图的平均距离通常不可行或非常耗时。
算法的相关资料如下:
- P. Boldi, M. Rosa, S. Vigna, HyperANF: Approximating the Neighbourhood Function of Very Large Graphs on a Budget (2011)
基本概念
图平均距离
图平均距离(Average Graph Distance)用于衡量图中任意两个节点之间的平均步数或边数。它量化了图中节点的整体连通性或接近程度。
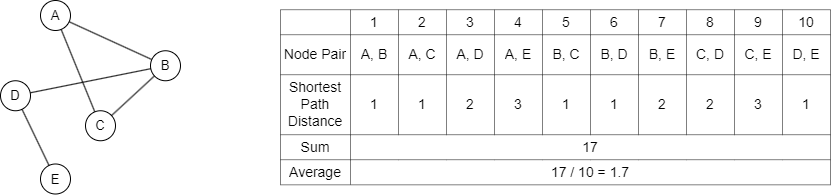
如上所示,计算图平均图距离通常通过执行图遍历来计算每对节点之间的最短路径距离,然后将距离求和并除以节点对的总数来得到平均值。
近似邻域函数(ANF)
对于大型图而言,图遍历通常会消耗大量的计算资源和内存,因此近似邻域函数(Approximate Neighborhood Function, ANF)算法常被用来更高效地估算图平均距离。
ANF算法旨在估算邻域函数(Neighborhood Function, NF):
- 图的邻域函数(NF),表示为
N(t),返回在t步内(含t)可以相互到达的节点对数量。 - 图中节点x的单点邻域函数(INF),表示为
N(x,t),返回从节点x出发,在t步内(含t)可以到达的节点数量。 - 在无向图G=(V, E)中,NF和INF之间存在以下关系:
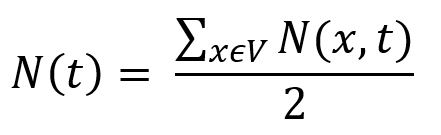
邻域函数可以揭示图的一些特征,其中包括图平均距离:
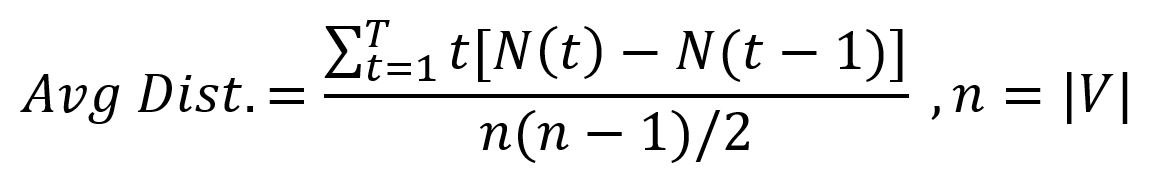
以下是通过邻域函数计算上述示例图的平均距离的过程:

然而,在大型图上精确计算邻域函数的成本非常高。通过估算邻域函数,ANF算法可以在不遍历整个图的情况下估算出图平均距离。
HyperLogLog计数器
HyperLogLog计数器用于近似计算大型集合或元素流中不同元素数量,即基数(Cardinality)。精确计算基数通常需要与基数成比例的内存量,这对于超大数据集来说是不切实际的。HyperLogLog使用的内存则要少得多,其空间复杂度为O(log(log n))(因而得名HyperLogLog)。
一个HyperLogLog计数器可以看作是一个包含m=2b个寄存器(Register)的数组,每个寄存器的值被初始化为 -∞。例如,当b=3时,M[0]=M[1]=...=M[7]=-∞。
寄存器的数量取决于所需估计的精度。更多的寄存器可以提供更准确的估计,但也需要更多的内存。
首先,集合中的每个元素x通过一个哈希函数h()映射为一个固定大小的二进制序列。例如,h(x)=0100001110101...。
然后,更新寄存器。对于集合中的每个元素x:
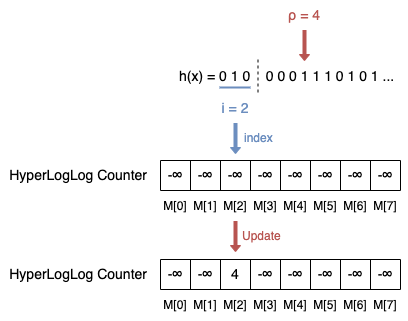
- 通过取h(x)最左边b位(记作hb(x))的整数值计算寄存器的索引i。在本例中,i=hb(x)=010=0*22+1*21+0*20=2。
- 令hb(x)为h(x)的剩余位序列,ρ(hb(x))为hb(x)的最左边1的位置。在本例中,ρ(hb(x))=ρ(0001110101...)=4。
- 更新寄存器M[i]=max(M[i], ρ(hb(x)))。在本例中,M[2]=max(-∞, 4)=4。
读取所有元素后,通过HyperLogLog计数器计算基数如下:
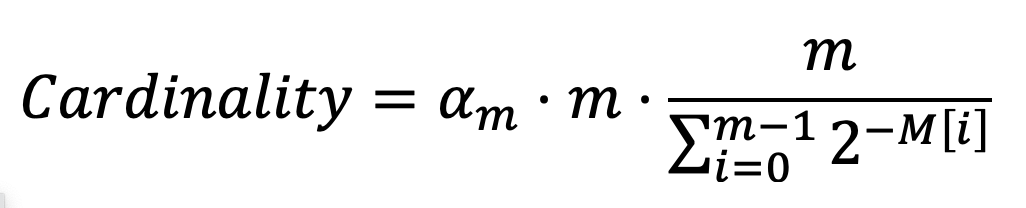
这实际上是对2M[i]的调和平均数进行归一化处理,其中αm是根据m的值计算得出的常数:
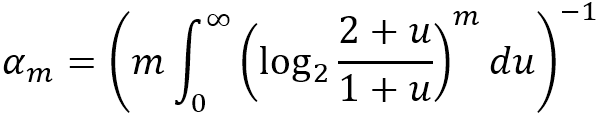
HyperANF
HyperANF是一种流行的ANF算法,它在速度和可扩展性方面取得了突破性的改进。
该算法基于以下观察结果:距离节点x在t步以内(含t)的节点集合B(x,t)满足以下条件:
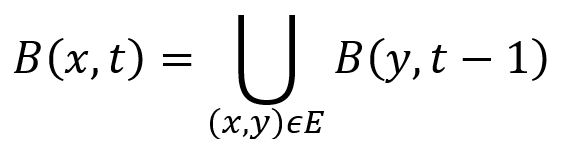
在下面的示例图中,节点a有三条邻边,分别是(a,b)、(a,c)和(a,d),因此B(a,3) = B(b,2) ∪ B(c,2) ∪ B(d,2)。
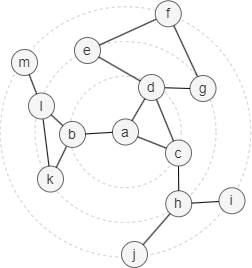
对于每个节点x,HyperANF算法使用HyperLogLog计数器简化计算过程。以下使用上面的示例图具体说明:
- 将每个节点x映射到一个二进制表示h(x),并分配一个HyperLogLog计数器Cx(t)。假设b=2,则每个计数器有m=2b=4个寄存器。
- 然后可根据i和ρ的值计算Cx(0)。注意:我们使用0代替-∞,结果是一样的。
- 在第t次迭代中,对于每个节点x,通过合并节点x的所有邻居的计数器来实现
B(y,t-1)((x,y)∈E)的并集,即逐个寄存器地将节点x的计数器的值最大化。 - 经过6次迭代后,所有计数器的值保持不变,实际上是因为图的直径为6。
- 在每次迭代中,通过带有常量αm=0.53243的基数方程计算
|B(x,t)|。
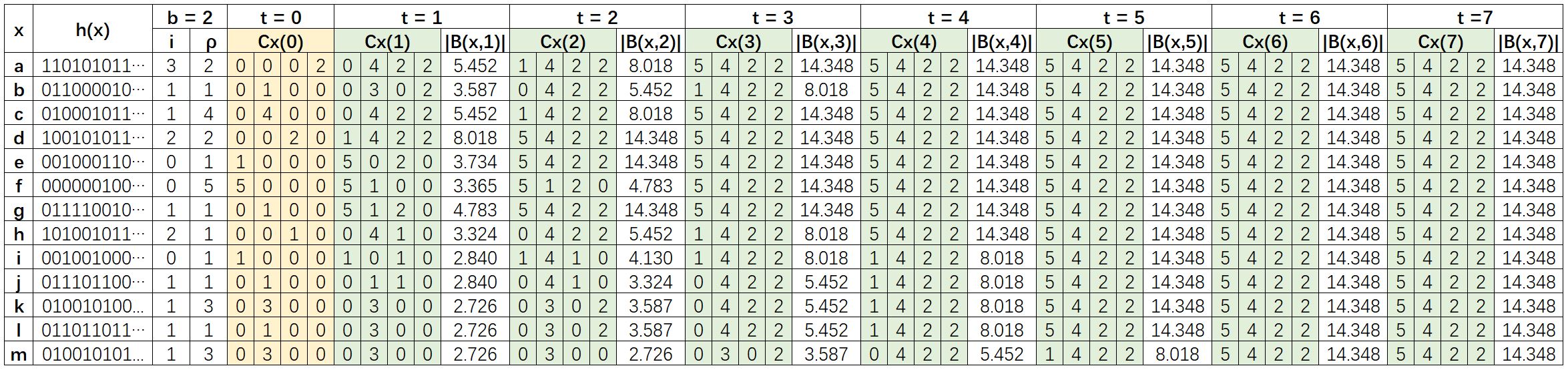
由于B(x,0) = {x},因此|N(x,t)| = |B(x,t)| - 1。在这个例子中,通过算法计算得到的平均图距离是3.2041。这个例子的精确平均图距离是3。
特殊说明
- HyperANF算法通常最适用于连通图。对于非连通图,该算法可能无法提供准确的结果。
- HyperANF算法忽略边的方向,按照无向边进行计算。
示例图
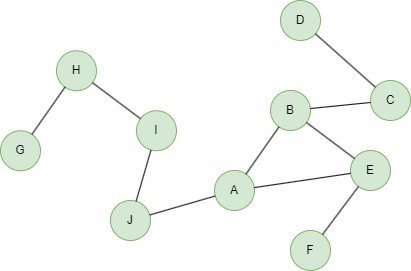
在一个空图中运行以下语句定义图结构并插入数据:
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(H:default {_id: "H"}),
(I:default {_id: "I"}),
(J:default {_id: "J"}),
(G)-[:default]->(H),
(H)-[:default]->(I),
(I)-[:default]->(J),
(J)-[:default]->(A),
(A)-[:default]->(B),
(A)-[:default]->(E),
(E)-[:default]->(F),
(B)-[:default]->(E),
(B)-[:default]->(C),
(C)-[:default]->(D);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}, {_id:"H"}, {_id:"I"}, {_id:"J"}]);
insert().into(@default).edges([{_from:"G", _to:"H"}, {_from:"H", _to:"I"}, {_from:"I", _to:"J"}, {_from:"J", _to:"A"}, {_from:"A", _to:"B"}, {_from:"A", _to:"E"}, {_from:"E", _to:"F"}, {_from:"B", _to:"E"}, {_from:"B", _to:"C"}, {_from:"C", _to:"D"}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:hyperANF
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
loop_num |
Integer | ≥1 | / | 否 | 最大迭代轮数。算法将在完成所有轮次后停止 |
register_num |
Integer | [4,30] | / | 否 | 决定HyperLogLog计数器中寄存器数量(m = 2b)的b值 |
文件回写
CALL algo.hyperANF.write("my_hdc_graph", {
loop_num: 5,
register_num: 4
}, {
file: {
filename: "distance"
}
})
algo(hyperANF).params({
projection: "my_hdc_graph",
loop_num: 5,
register_num: 4
}).write({
file: {
filename: "distance"
}
})
hyperANF_result: 2.46228
统计回写
CALL algo.hyperANF.write("my_hdc_graph", {
loop_num: 5,
register_num: 4
}, {
stats: {}
})
algo(hyperANF).params({
projection: "my_hdc_graph",
loop_num: 5,
register_num: 4
}).write({
stats: {}
})
结果:
| hyperANF_result |
|---|
| 2.462277 |
完整返回
CALL algo.hyperANF.run("my_hdc_graph", {
loop_num: 5,
register_num: 4
}) YIELD distance
RETURN distance
exec{
algo(hyperANF).params({
loop_num: 5,
register_num: 4
}) as distance
return distance
} on my_hdc_graph
结果:
| hyperANF_result |
|---|
| 2.462276 |
流式返回
CALL algo.hyperANF.stream("my_hdc_graph", {
loop_num: 7,
register_num: 5
}) YIELD distance
RETURN round(distance.hyperANF_result)
exec{
algo(hyperANF).params({
loop_num: 7,
register_num: 10
}).stream() as distance
return round(distance.hyperANF_result)
} on my_hdc_graph
结果:
| round(distance.hyperANF_result) |
|---|
| 3 |
统计返回
CALL algo.hyperANF.stats("my_hdc_graph", {
loop_num: 7,
register_num: 10
}) YIELD distance
RETURN distance
exec{
algo(hyperANF).params({
loop_num: 7,
register_num: 10
}).stats() as result
return result
} on my_hdc_graph
结果:
| bipartite_result |
|---|
| 2.903838 |
