概述
k-Core算法能识别图中最大的连通子图,其中所有节点的度不小于 k。它常用来识别和提取图中紧密连通的群组,以便做进一步分析。该算法广泛应用于金融风险控制、社交网络分析和生物学等多个研究领域。k-Core算法的主要优势之一是时间复杂度低(线性),因此能高效地处理大型图。此外,k-Core生成的子图具有良好的直观可解释性,有助于理解图的结构模式和关系。
普遍接受的k-Core概念最早是由Seidman提出的:
- S.B. Seidman, Network Structure And Minimum Degree. Soc Netw 5:269-287 (1983)
基本概念
k-Core
图的k-Core子图是通过迭代剪枝过程得到的。从原图开始,按顺序反复从图中去掉度小于k的节点,直到剩余节点的度均大于或等于k。
以下是获取图的3-core子图的修剪过程。在第一轮中,度数小于3的节点{a, d, f}被移除,这影响到节点b在第二轮中被移除。第二轮之后,所有剩余节点的度数都不少于3,因此修剪过程结束,该图的3-core是由节点{c, e, g, h}诱导的。

嬴图的k-Core算法识别图中每个连通分量的k-core子图。
特殊说明
- k-Core算法忽略图中的自环边。在计算相应节点的度时,不考虑它的自环边。
- k-Core算法忽略边的方向,按照无向边进行计算。
示例图
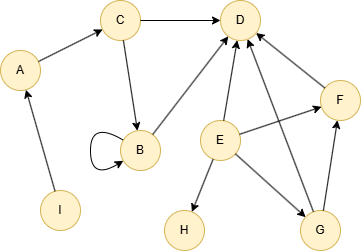
在一个空图中运行以下语句定义图结构并插入数据:
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(H:default {_id: "H"}),
(I:default {_id: "I"}),
(A)-[:default]->(C),
(B)-[:default]->(B),
(B)-[:default]->(D),
(C)-[:default]->(B),
(C)-[:default]->(D),
(E)-[:default]->(D),
(E)-[:default]->(F),
(E)-[:default]->(G),
(E)-[:default]->(H),
(F)-[:default]->(D),
(G)-[:default]->(D),
(G)-[:default]->(F),
(I)-[:default]->(A);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}, {_id:"H"}, {_id:"I"}]);
insert().into(@default).edges([{_from:"A", _to:"C"}, {_from:"B", _to:"B"}, {_from:"B", _to:"D"}, {_from:"C", _to:"B"}, {_from:"C", _to:"D"}, {_from:"E", _to:"D"}, {_from:"E", _to:"F"}, {_from:"E", _to:"G"}, {_from:"E", _to:"H"}, {_from:"F", _to:"D"}, {_from:"G", _to:"D"}, {_from:"G", _to:"F"}, {_from:"I", _to:"A"}]);
在HDC图上运行算法
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:k_core
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
k |
Integer | ≥1 | / | 否 | k-core子图中每个节点的最小度k |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点;该选项仅在文件回写模式下生效 |
文件回写
CALL algo.k_core.write("my_hdc_graph", {
k: 3,
return_id_uuid: "id"
}, {
file: {
filename: "3-core"
}
})
algo(k_core).params({
projection: "my_hdc_graph",
k: 3,
return_id_uuid: "id"
}).write({
file: {
filename: "3-core"
}
})
结果:
_id
G
F
E
D
完整返回
CALL algo.k_core.run("my_hdc_graph", {
k: 2
}) YIELD k2
RETURN k2
exec{
algo(k_core).params({
k: 2
}) as result
return result
} on my_hdc_graph
[{"id":"G","uuid":"13690943966717935617","schema":"default","values":{}}]
[{"id":"D","uuid":"288231475663339522","schema":"default","values":{}}]
[{"id":"F","uuid":"2882304861028745219","schema":"default","values":{}}]
[{"id":"B","uuid":"3530823207370096641","schema":"default","values":{}}]
[{"id":"E","uuid":"10520409829049106435","schema":"default","values":{}}]
[{"id":"C","uuid":"12033619303845593090","schema":"default","values":{}}]
流式返回
CALL algo.k_core.stream("my_hdc_graph", {
k: 3
}) YIELD r
FOR node in r
RETURN node._id
exec{
algo(k_core).params({
k: 3
}).stream() as r
uncollect r as node
return node._id
} on my_hdc_graph
结果:
| node._id |
|---|
| G |
| D |
| F |
| E |
在分布式投影上运行算法
创建分布式投影
将图集全部投影到shard服务器上并命名为myProj:
CREATE PROJECTION myProj OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true
}
create().projection("myProj", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true
})
参数
算法名:k_core
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
k |
Integer | ≥1 | / | 否 | k-Core子图中,每个节点的最小度为k |
文件回写
CALL algo.k_core.write("myProj", {
k: 3
}, {
file: {
filename: "3-core"
}
})
algo(k_core).params({
projection: "myProj",
k: 3
}).write({
file: {
filename: "3-core"
}
})
_id
E
D
F
G
