概述
K边连通分量(k-Edge Connected Components)算法旨在根据图中的边来识别具有强关联的节点组。该算法关注的是边的连接情况,以揭示图中节点之间的紧密关系和群组结构。通过考虑边的连通性,该算法能够识别出在图中形成紧密连接的节点组,这些节点组可能代表着社区、集群或其他相关的结构。
算法的相关资料如下:
- T. Wang, Y. Zhang, F.Y.L. Chin, H. Ting, Y.H. Tsin, S. Poon, A Simple Algorithm for Finding All k-Edge-Connected Components (2015)
基本概念
边连通性
图的边连通性(Edge Connectivity)是指为降低或破坏图的连通性所需移除的最小边数。换句话说,它表示了图在面对边的缺失或故障时能够恢复到连通状态的能力。对于给定的图G=(V, E),如果在删除任意k-1或更少条边后,图G仍然保持连通,则称图G具有k边连通性。
边连通性也可以理解为图中任意两个节点之间的边不相交路径(Edge-disjoint Paths)的最大数量。如果图的边连通性为k,则表示图中任意一对节点之间存在k条边不相交路径。
下面展示的是一个具有3边连通性的图以及每对节点之间的所有边不相交路径。
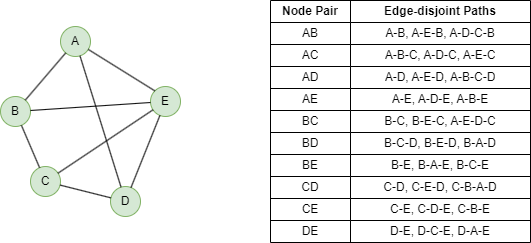
一组边不相交路径是指它们没有任何共同边。
K 边连通分量
K边连通分量算法的目标不是确定全图G是否具有k边连通性,而是要找到图中具有k边连通性的最大节点子集Vi⊆V,由Vi诱导的子图具有k边连通性。
举例来说,在社交网络中,我们可能更感兴趣的是发现那些紧密联系的人群,而不是计算整个社交网络的全局连通性。
特殊说明
- 当k=1时,相当于寻找图的连通分量。
- K边连通分量算法忽略边的方向,按照无向边进行计算。
示例图
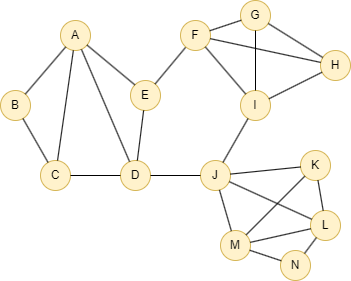
在一个空图中运行以下语句定义图结构并插入数据:
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(H:default {_id: "H"}),
(I:default {_id: "I"}),
(J:default {_id: "J"}),
(K:default {_id: "K"}),
(L:default {_id: "L"}),
(M:default {_id: "M"}),
(N:default {_id: "N"}),
(A)-[:default]->(B),
(B)-[:default]->(C),
(A)-[:default]->(C),
(A)-[:default]->(D),
(A)-[:default]->(E),
(C)-[:default]->(D),
(E)-[:default]->(D),
(E)-[:default]->(F),
(D)-[:default]->(J),
(F)-[:default]->(G),
(F)-[:default]->(I),
(G)-[:default]->(H),
(F)-[:default]->(H),
(G)-[:default]->(I),
(H)-[:default]->(I),
(I)-[:default]->(J),
(J)-[:default]->(K),
(J)-[:default]->(M),
(K)-[:default]->(L),
(J)-[:default]->(L),
(M)-[:default]->(K),
(M)-[:default]->(L),
(M)-[:default]->(N),
(N)-[:default]->(L);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}, {_id:"H"}, {_id:"I"}, {_id:"J"}, {_id:"K"}, {_id:"L"}, {_id:"M"}, {_id:"N"}]);
insert().into(@default).edges([{_from:"A", _to:"B"}, {_from:"B", _to:"C"}, {_from:"A", _to:"C"}, {_from:"A", _to:"D"}, {_from:"A", _to:"E"}, {_from:"C", _to:"D"}, {_from:"E", _to:"D"}, {_from:"E", _to:"F"}, {_from:"D", _to:"J"}, {_from:"F", _to:"G"}, {_from:"F", _to:"I"}, {_from:"G", _to:"H"}, {_from:"F", _to:"H"}, {_from:"G", _to:"I"}, {_from:"H", _to:"I"}, {_from:"I", _to:"J"}, {_from:"J", _to:"K"}, {_from:"J", _to:"M"}, {_from:"K", _to:"L"}, {_from:"J", _to:"L"}, {_from:"M", _to:"K"}, {_from:"M", _to:"L"}, {_from:"M", _to:"N"}, {_from:"N", _to:"L"}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:kcc
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
k |
Integer | >1 | / | 否 | K边连通分量中,任意一对节点间存在k条边不相交路径 |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点 |
文件回写
CALL algo.kcc.write("my_hdc_graph", {
k: 3,
return_id_uuid: "id"
}, {
file: {
filename: "kcc_result"
}
})
algo(kcc).params({
projection: "my_hdc_graph",
k: 3,
return_id_uuid: "id"
}).write({
file: {
filename: "kcc_result"
}
})
_ids
M,J,K,L
G,F,H,I
