概述
K均值(k-Means)算法是一种广泛使用的聚类算法,旨在根据节点的相似性将图中的节点分为k个聚类。该算法将每个节点分配至距离最近的质心所在的聚类。节点和质心之间的距离可以使用不同的度量方法来计算,例如欧几里得距离或余弦相似性。
K均值算法的概念可以追溯至1957年,它在1967年由J. MacQueen正式命名和推广:
- J. MacQueen, Some methods for classification and analysis of multivariate observations (1967)
从那时起,该算法在各个领域都有应用,包括向量量化、聚类分析、特征学习、计算机视觉等。它通常用作其他算法的预处理步骤,或作为数据分析的独立方法来使用。
基本概念
质心
一个N维空间中对象的质心(Centroid)或几何中心是所有N个坐标方向上点的平均位置。
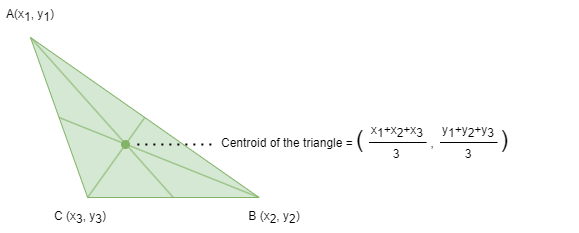
在K均值这类聚类算法的语境中,质心是指聚类的几何中心。通过将多个节点属性指定为节点特征,质心是汇总了聚类中所有节点特征的代表性点。为了找到聚类的质心,该算法计算该聚类中所有节点每个维度的平均特征值。
K均值算法以k个节点作为初始质心,可以手动指定或由系统随机采样。
距离度量指标
嬴图的K均值算法可以计算节点与质心之间的欧几里得距离或余弦相似度。
聚类迭代
在K均值算法的每次迭代中,先计算图中每个节点到每个聚类质心的距离,然后并将节点分配给与其距离最近的聚类;将所有节点归到聚类中后,通过分配给每个聚类的节点重新计算聚类的质心。
如果聚类结果的变化低于预设的阈值,或达到了迭代次数限制,算法迭代就会结束。
特殊说明
- 适当选择k的值以及使用符合特定场景的距离度量指标对于K均值算法的结果至关重要。初始质心的选择也会影响最终的聚类结果。
- 如果存在两个或多个相同的质心,只有一个质心将生效,其余等效质心的聚类为空。
示例图
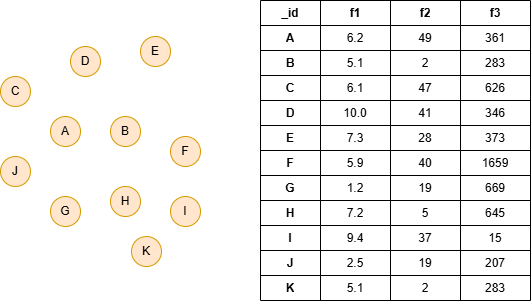
在一个空图中运行以下语句定义图结构并插入数据:
ALTER NODE default ADD PROPERTY {
f1 float, f2 int32, f3 int32
};
INSERT (:default {_id:"A", f1:6.2, f2:49, f3:361}),
(:default {_id:"B", f1:5.1, f2:2, f3:283}),
(:default {_id:"C", f1:6.1, f2:47, f3:626}),
(:default {_id:"D", f1:10.0, f2:41, f3:346}),
(:default {_id:"E", f1:7.3, f2:28, f3:373}),
(:default {_id:"F", f1:5.9, f2:40, f3:1659}),
(:default {_id:"G", f1:1.2, f2:19, f3:669}),
(:default {_id:"H", f1:7.2, f2:5, f3:645}),
(:default {_id:"I", f1:9.4, f2:37, f3:15}),
(:default {_id:"J", f1:2.5, f2:19, f3:207}),
(:default {_id:"K", f1:5.1, f2:2, f3:283});
create().node_property(@default,"f1",float).node_property(@default,"f2",int32).node_property(@default,"f3",int32);
insert().into(@default).nodes([{_id:"A", f1:6.2, f2:49, f3:361}, {_id:"B", f1:5.1, f2:2, f3:283}, {_id:"C", f1:6.1, f2:47, f3:626}, {_id:"D", f1:10.0, f2:41, f3:346}, {_id:"E", f1:7.3, f2:28, f3:373}, {_id:"F", f1:5.9, f2:40, f3:1659}, {_id:"G", f1:1.2, f2:19, f3:669}, {_id:"H", f1:7.2, f2:5, f3:645}, {_id:"I", f1:9.4, f2:37, f3:15}, {_id:"J", f1:2.5, f2:19, f3:207}, {_id:"K", f1:5.1, f2:2, f3:283}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:k_means
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
start_ids |
[]_id |
/ | / | 是 | 通过_id指定点作为初始质心;数组长度为k。若未设置,则由系统自行选取 |
start_uuids |
[]_uuid |
/ | / | 是 | 通过_id指定点作为初始质心;数组长度为k。若未设置,则由系统自行选取 |
k |
Integer | [1, |V|] |
1 |
否 | 指定聚类总数(|V|是图集中的总点数) |
distance_type |
Integer | 1, 2 |
1 |
是 | 指定距离度量指标类型:设置为1时,计算欧几里得距离;设置为2时,计算余弦相似度 |
node_schema_property |
[]"<@schema.?><property>" |
/ | / | 否 | 作为特征的数值类型点属性;需包含至少两个属性 |
loop_num |
Integer | ≥1 | / | 否 | 最大迭代轮数。算法将在完成所有轮次后停止 |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点 |
文件回写
CALL algo.k_means.write("my_hdc_graph", {
return_id_uuid: "id",
start_ids: ["A", "B", "E"],
k: 3,
distance_type: 2,
node_schema_property: ["f1", "f2", "f3"],
loop_num: 3
}, {
file: {
filename: "communities"
}
})
algo(k_means).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
start_ids: ["A", "B", "E"],
k: 3,
distance_type: 2,
node_schema_property: ["f1", "f2", "f3"],
loop_num: 3
}).write({
file: {
filename: "communities"
}
})
结果:
community id:ids
0:I
1:F,H,B,K,G
2:J,D,A,E,C
Full Return
CALL algo.k_means.run("my_hdc_graph", {
return_id_uuid: "id",
start_ids: ["A", "B", "E"],
k: 3,
distance_type: 1,
node_schema_property: ["f1", "f2", "f3"],
loop_num: 3
}) YIELD k3
RETURN k3
exec{
algo(k_means).params({
return_id_uuid: "id",
start_ids: ["A", "B", "E"],
k: 3,
distance_type: 1,
node_schema_property: ["f1", "f2", "f3"],
loop_num: 3
}) as k3
return k3
} on my_hdc_graph
结果:
| community | _ids |
|---|---|
| 0 | ["D","B","A","E","K"] |
| 1 | ["J","I"] |
| 2 | ["F","H","C","G"] |
流式返回
CALL algo.k_means.stream("my_hdc_graph", {
return_id_uuid: "id",
k: 2,
node_schema_property: ["f1", "f2", "f3"],
loop_num: 5
}) YIELD k2
RETURN k2
exec{
algo(k_means).params({
return_id_uuid: "id",
k: 2,
node_schema_property: ["f1", "f2", "f3"],
loop_num: 5
}).stream() as k2
return k2
} on my_hdc_graph
结果:
| community | _ids |
|---|---|
| 0 | ["J","D","B","A","E","K","I"] |
| 1 | ["F","H","C","G"] |
