概述
Leiden(莱顿)是一种旨在最大化模块度的社区识别算法。它是为了解决广泛使用的Louvain算法可能存在的社区内部连通性不良甚至不连通的问题而提出的。另外,Leiden比Louvain效率更高。该算法是以其作者所在地命名的。
参考资料:
- V.A. Traag, L. Waltman, N.J. van Eck, From Louvain to Leiden: guaranteeing well-connected communities (2019)
- V.A. Traag, P. Van Dooren, Y. Nesterov, Narrow scope for resolution-limit-free community detection (2011)
基本概念
模块度
模块度(Modularity)的概念在Louvain算法中有所介绍。Leiden算法在模块度公式中引入了一个新的分辨率参数γ(gamma):
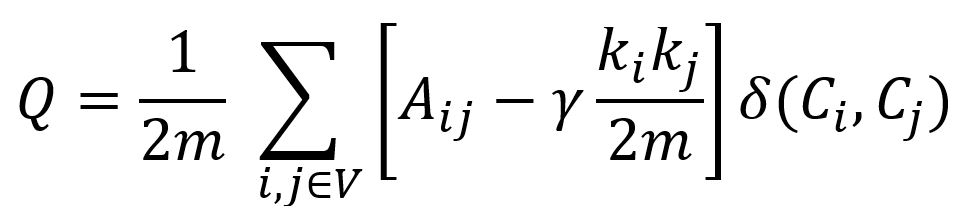
参数γ调节社区内部和社区之间连接密度:
- 当
γ> 1时,会形成更多、更小且连接紧密的社区。 - 当0 <
γ< 1时,会形成更少、更大但连接相对不那么紧密的社区。
Leiden
Leiden算法开始时,图中每个点都是一个社区。算法进行多次迭代,每轮迭代由三个阶段组成。
第一阶段:快速模块度优化
Louvain算法在第一阶段会重复遍历图中所有点,直到没有任何点的社区移动能提升模块度。Leiden算法采用一种更高效的方法,它遍历完图中所有点后,只再次遍历那些邻居点发生了变化的点。
为了实现这一点,Leiden算法使用一个队列,初始化时随机将图中所有点添加到队列中。然后,重复以下步骤直到队列为空:
- 从队列最前端移除一个点
v。 - 将点
v分配至能获得最大模块度增益(ΔQ)的新社区C;如果加入任何社区都不能获得大于0的增益,则保留该节点在原社区。 - 如果点
v被移动到新社区C,将所有不属于C且不在队列中的v的邻居点添加到队列尾端。
第二阶段:社区优化
本阶段根据第一阶段得到的社区划分P,得到另一种社区划分Prefined。初始化Prefined时,原图或聚合图中的每个点都是一个社区。接着,针对P中的每个社区C:
1. 根据下式找到C内部连接良好的点v:
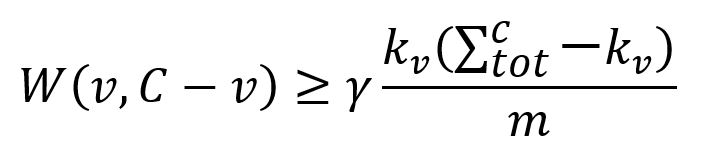
其中,
W(v, C-v)是点v与社区C中其他点相连的边的权重和。kv与点v相连的边的权重和。是社区C所有点的k值和。m是图中所有边的权重和。
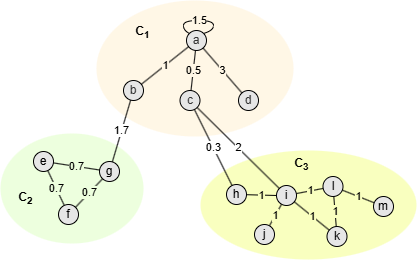
以上图中的社区C1为例,其中
- m = 18.1
- = ka + kb + kc + kd = 6 + 2.7 + 2.8 + 3 = 14.5
如果γ为1.2,则:
- W(a, C1) - γ/m ⋅ ka ⋅ (
∑ tot C 1 - W(b, C1) - γ/m ⋅ kb ⋅ (
∑ tot C 1 - W(c, C1) - γ/m ⋅ kc ⋅ (
∑ tot C 1 - W(d, C1) - γ/m ⋅ kd ⋅ (
∑ tot C 1
因此,我们认为社区C1中点a和d是连接良好的。
2. 访问上一步找到的每个连接良好的点v,如果它在Prefined中仍处于自己独立的社区,随机将其合并到一个能使模块度增加的社区C'∈Prefined,同时C'必须与C连接良好,判断条件如下:
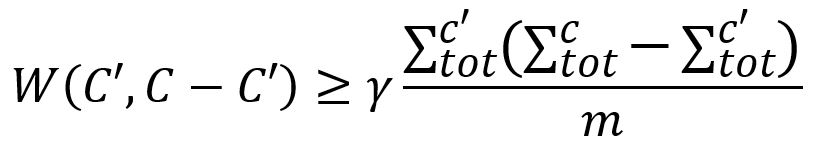
注意,每个点v并不贪心地与产生最大模块度增益的社区合并。然而,与某个社区合并产生的增益越大,该社区被选择的可能性越大。选择社区C'的随机程度由参数θ(theta)决定:
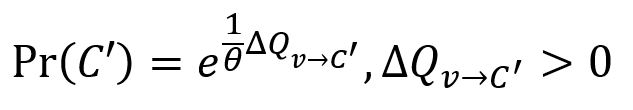
在社区合并过程中引入随机性,可以更广泛地探索分区空间。
第三阶段:社区聚合
基于Prefined进行社区聚合,方法同Louvain。请注意,在Louvain算法的聚合图中,每个点属于单独的社区;而在Leiden算法中,基于P考虑聚合图中的社区划分,可能有多个点属于同一社区。
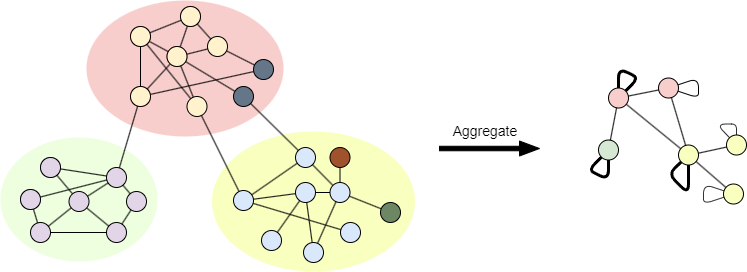
P用颜色区块表示,Prefined用节点颜色表示完成第三阶段后,基于聚合图进行下一次迭代。迭代会一直进行,直至点的所属社区没有任何变化,达到最大模块度。
特殊说明
- 如果节点
v有自环边,计算kv时,自环边的权重只计算一次。 - Leiden算法忽略边方向。
示例图
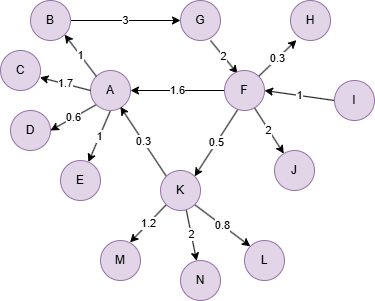
在一个空图中运行以下语句定义图结构并插入数据:
ALTER EDGE default ADD PROPERTY {
weight float
};
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(H:default {_id: "H"}),
(I:default {_id: "I"}),
(J:default {_id: "J"}),
(K:default {_id: "K"}),
(L:default {_id: "L"}),
(M:default {_id: "M"}),
(N:default {_id: "N"}),
(A)-[:default {weight: 1}]->(B),
(A)-[:default {weight: 1.7}]->(C),
(A)-[:default {weight: 0.6}]->(D),
(A)-[:default {weight: 1}]->(E),
(B)-[:default {weight: 3}]->(G),
(F)-[:default {weight: 1.6}]->(A),
(F)-[:default {weight: 0.3}]->(H),
(F)-[:default {weight: 2}]->(J),
(F)-[:default {weight: 0.5}]->(K),
(G)-[:default {weight: 2}]->(F),
(I)-[:default {weight: 1}]->(F),
(K)-[:default {weight: 0.3}]->(A),
(K)-[:default {weight: 0.8}]->(L),
(K)-[:default {weight: 1.2}]->(M),
(K)-[:default {weight: 2}]->(N);
create().edge_property(@default, "weight", float);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}, {_id:"H"},{_id:"I"},{_id:"J"},{_id:"K"},{_id:"L"},{_id:"M"},{_id:"N"}]);
insert().into(@default).edges([{_from:"A", _to:"B", weight:1}, {_from:"A", _to:"C", weight:1.7}, {_from:"A", _to:"D", weight:0.6}, {_from:"A", _to:"E", weight:1}, {_from:"B", _to:"G", weight:3}, {_from:"F", _to:"A", weight:1.6}, {_from:"F", _to:"H", weight:0.3}, {_from:"F", _to:"J", weight:2}, {_from:"F", _to:"K", weight:0.5}, {_from:"G", _to:"F", weight:2}, {_from:"I", _to:"F", weight:1}, {_from:"K", _to:"A", weight:0.3}, {_from:"K", _to:"M", weight:1.2}, {_from:"K", _to:"N", weight:2}, {_from:"K", _to:"L", weight:0.8}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:leiden
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
phase1_loop_num |
Integer | ≥1 | 5 |
是 | 每轮迭代第一阶段的最大循环次数 |
min_modularity_increase |
Float | [0,1] | 0.01 |
是 | 将点分配到另一社区的最小模块度增益(ΔQ) |
edge_schema_property |
[]"<@schema.?><property>" |
/ | / | 是 | 作为权重的数值类型边属性,权重值为所有指定属性值的总和;不包含指定属性的边将被忽略 |
gamma |
Float | >0 | 1 | 是 | 分辨率参数γ |
theta |
Float | ≥0 | 0.01 | 是 | 第二阶段社区合并时,控制随机程度的参数θ;设为0不随机,取模块度增益最大的社区 |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点 |
limit |
Integer | ≥-1 | -1 |
是 | 限制返回的结果数;-1返回所有结果 |
order |
String | asc, desc |
/ | 是 | 根据count值对结果排序;该选项仅在流式返回模式下mode为2时生效 |
文件回写
该算法可生成三个文件:
配置项 |
内容 |
|---|---|
filename_community_id |
|
filename_ids |
|
filename_num |
|
CALL algo.leiden.write("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}, {
file: {
filename_community_id: "f1",
filename_ids: "f2",
filename_num: "f3"
}
})
algo(leiden).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}).write({
file: {
filename_community_id: "f1",
filename_ids: "f2",
filename_num: "f3"
}
})
结果:
_id,community_id
I,5
G,7
J,5
D,9
N,11
F,5
H,5
B,7
L,11
A,9
E,9
K,11
M,11
C,9
community_id,_ids
5,I;J;F;H;
7,G;B;
9,D;A;E;C;
11,N;L;K;M;
community_id,count
5,4
7,2
9,4
11,4
数据库回写
将结果中的community_id值写入指定点属性。该属性类型为uint32。
CALL algo.leiden.write("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}, {
db: {
property: "communityID"
}
})
algo(leiden).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}).write({
db: {
property: 'communityID'
}
})
统计回写
CALL algo.leiden.write("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}, {
stats: {}
})
algo(leiden).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}).write({
stats: {}
})
结果:
| community_count | modularity |
|---|---|
| 4 | 0.548490 |
完整返回
CALL algo.leiden.run("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1
}) YIELD r
RETURN r
exec {
algo(leiden).params({
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1
}) as r
return r
} on hdc_leiden
结果:
| _id | community_id |
|---|---|
| I | 5 |
| G | 7 |
| J | 5 |
| D | 9 |
| N | 11 |
| F | 5 |
| H | 5 |
| B | 7 |
| L | 11 |
| A | 9 |
| E | 9 |
| K | 11 |
| M | 11 |
| C | 9 |
流式返回
流式返回支持两种模式:
| 项目 | 配置项 | 列名 |
|---|---|---|
mode |
1(默认) |
|
2 |
|
CALL algo.leiden.stream("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 6,
min_modularity_increase: 0.1
}) YIELD r
RETURN r
exec{
algo(leiden).params({
return_id_uuid: "id",
phase1_loop_num: 6,
min_modularity_increase: 0.1
}).stream() as r
return r
} on my_hdc_graph
结果:
| _id | community_id |
|---|---|
| I | 5 |
| G | 7 |
| J | 5 |
| D | 9 |
| N | 11 |
| F | 5 |
| H | 5 |
| B | 7 |
| L | 11 |
| A | 9 |
| E | 9 |
| K | 11 |
| M | 11 |
| C | 9 |
CALL algo.leiden.stream("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 6,
min_modularity_increase: 0.1
}, {
mode: 2
}) YIELD r
RETURN r
exec{
algo(leiden).params({
return_id_uuid: "id",
phase1_loop_num: 6,
min_modularity_increase: 0.1,
order: "asc"
}).stream({
mode: 2
}) as r
return r
} on my_hdc_graph
结果:
| community_id | count |
|---|---|
| 7 | 2 |
| 5 | 4 |
| 9 | 4 |
| 11 | 4 |
统计返回
CALL algo.leiden.stats("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 6,
min_modularity_increase: 0.1
}) YIELD s
RETURN s
exec{
algo(leiden).params({
return_id_uuid: "id",
phase1_loop_num: 6,
min_modularity_increase: 0.1
}).stats() as s
return s
} on my_hdc_graph
结果:
| community_count | modularity |
|---|---|
| 4 | 0.397778 |
