概述
Louvain(鲁汶)是一个广受认可和应用的社区识别算法,它是以其作者的位置命名的——来自比利时鲁汶天主教大学的Vincent D. Blondel等人。该算法是以最大化图的模块度(Modularity)为首要目标进行计算的,并且由于其较高的效率和优质的结果而受到欢迎。
- V.D. Blondel, J. Guillaume, R. Lambiotte, E. Lefebvre, Fast unfolding of communities in large networks (2008)
- H. Lu, Parallel Heuristics for Scalable Community Detection (2014)
基本概念
模块度
在许多网络中,节点自然地会形成群组或社区(Community),特点是社区内的节点连接密集,而社区之间的连接则较稀疏。
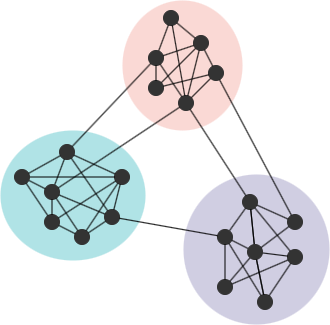
考虑一个与G对应的等价网络G'。在G'中,社区划分和边的总数与G中相同,但边是随机放置的。如果G表现出良好的社区结构,G中社区内部的边数与总边数之比应该高于G'中预期的比例。实际比例与预期值之间的差异越大,说明在G中的社区结构越显著。这就是模块度(Modularity)的原始概念。模块度是评估社区划分质量的最广泛使用的方法之一,Louvain算法就是旨在找到使得模块度最大的社区划分结果。
模块度的取值范围为-1到1。接近1的值表示更明显的社区结构,而负值则意味着划分不具有意义。对于连通图,模块度的取值范围为-0.5到1。
考虑图中边的权重,模块度(Q)的定义如下:
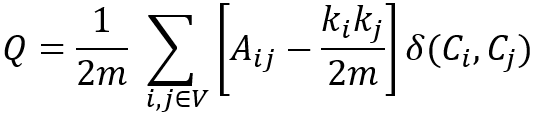
其中,
- m是图中所有边的权重之和;
- Aij是节点i和节点j之间边的权重和,且2m = ∑ijAij;
- ki是与节点i相连的所有边的权重之和;
- Ci表示节点i所属的社区,当Ci = Cj时,δ(Ci, Cj)为1,否则为0。
请留意,是节点i和j之间随机放置边时的预期边权重之和,Aij和
我们也可以将上式写成如下形式:
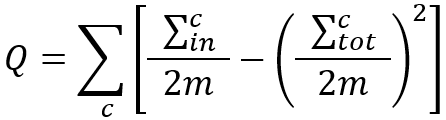
其中,
∑ in c ∑ tot c - m的含义与上面相同,且2m = ∑c
∑ tot c
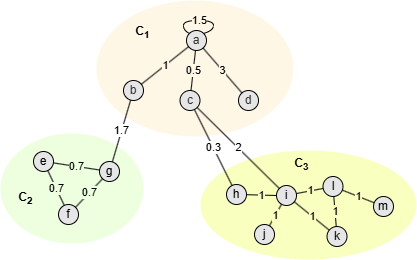
上图中的节点被划分至3个社区,以社区C1为例:
∑ in C 1 - (
∑ tot C 1
Louvain
Louvain算法开始时,图中的每个节点都在自己的社区中。然后算法进行多次迭代,每轮迭代由两个阶段组成。
第一阶段:模块度优化
对于每个节点i,考虑其邻居节点j,计算将节点i从当前社区重新分配到节点j所在的社区而产生的模块度增益(ΔQ)。
当ΔQ大于预设的正阈值时,将节点i放入使ΔQ最大的社区中。如果无法达到预设的增益,节点i则留在原来的社区中。
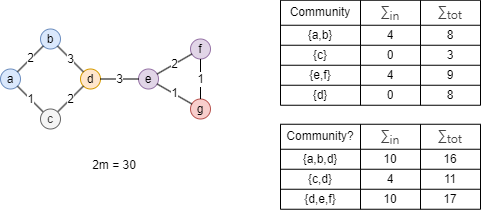
以上图为例,当前在同一社区的节点用同一颜色表示。如果现在考虑节点d,将其重新分配至社区{a,b}、{c}或{e,f}分别所产生的模块度增益如下:
- ΔQd→{a,b} = Q{a,b,d} - (Q{a,b} + Q{d}) = 52/900
- ΔQd→{c} = Q{c,d} - (Q{c} + Q{d}) = 72/900
- ΔQd→{e,f} = Q{d,e,f} - (Q{e,f} + Q{d}) = 36/900
如果 ΔQd→{c}大于预设的模块度增益阈值,则将节点d移至社区{c},否则d仍留在原来的社区。
按顺序将这个过程应用于所有节点,并重复执行,直到没有任何节点的移动可以改善模块度,或者达到最大循环次数,第一阶段完成。
第二阶段:社区聚合
在第二阶段,每个社区被压缩成一个节点,每个聚合节点带有一条自环边,其权重等于社区内部权重。新节点之间边的权重是两个对应社区中节点之间边的权重之和。
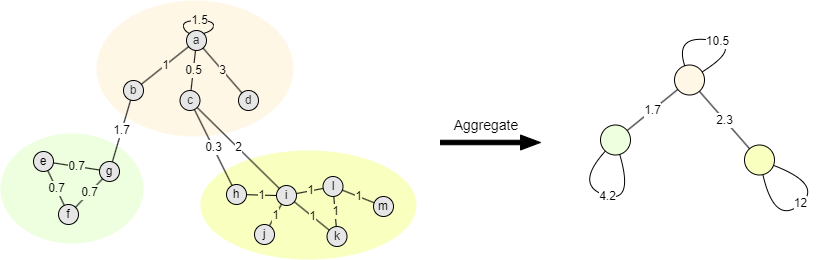
社区聚合减少了图中的节点和边的数量,同时保持局部及全图的权重度不变。聚合后,社区内的节点被视为一个整体,但它们不再是孤立地进行模块度优化,从而实现了分层(迭代)的社区划分效果。
完成第二阶段后,对聚合图进行另一次迭代。迭代会一直进行,直至没有任何变化,达到最大的模块度。
特殊说明
- 如果节点i存在自环边,计算ki 时,自环边的权重只计算一次。
- Louvain算法忽略边的方向,按照无向边进行计算。
- Louvain算法的输出结果可能会因为节点的考虑顺序不同而有所差异,但这不会对获得的模块度产生很大的影响。
示例图
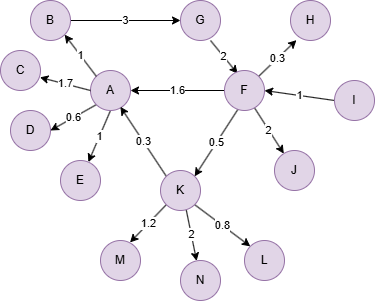
在一个空图中运行以下语句定义图结构并插入数据:
ALTER EDGE default ADD PROPERTY {
weight float
};
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(H:default {_id: "H"}),
(I:default {_id: "I"}),
(J:default {_id: "J"}),
(K:default {_id: "K"}),
(L:default {_id: "L"}),
(M:default {_id: "M"}),
(N:default {_id: "N"}),
(A)-[:default {weight: 1}]->(B),
(A)-[:default {weight: 1.7}]->(C),
(A)-[:default {weight: 0.6}]->(D),
(A)-[:default {weight: 1}]->(E),
(B)-[:default {weight: 3}]->(G),
(F)-[:default {weight: 1.6}]->(A),
(F)-[:default {weight: 0.3}]->(H),
(F)-[:default {weight: 2}]->(J),
(F)-[:default {weight: 0.5}]->(K),
(G)-[:default {weight: 2}]->(F),
(I)-[:default {weight: 1}]->(F),
(K)-[:default {weight: 0.3}]->(A),
(K)-[:default {weight: 0.8}]->(L),
(K)-[:default {weight: 1.2}]->(M),
(K)-[:default {weight: 2}]->(N);
create().edge_property(@default, "weight", float);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}, {_id:"H"},{_id:"I"},{_id:"J"},{_id:"K"},{_id:"L"},{_id:"M"},{_id:"N"}]);
insert().into(@default).edges([{_from:"A", _to:"B", weight:1}, {_from:"A", _to:"C", weight:1.7}, {_from:"A", _to:"D", weight:0.6}, {_from:"A", _to:"E", weight:1}, {_from:"B", _to:"G", weight:3}, {_from:"F", _to:"A", weight:1.6}, {_from:"F", _to:"H", weight:0.3}, {_from:"F", _to:"J", weight:2}, {_from:"F", _to:"K", weight:0.5}, {_from:"G", _to:"F", weight:2}, {_from:"I", _to:"F", weight:1}, {_from:"K", _to:"A", weight:0.3}, {_from:"K", _to:"M", weight:1.2}, {_from:"K", _to:"N", weight:2}, {_from:"K", _to:"L", weight:0.8}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:louvain
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
phase1_loop_num |
Integer | ≥1 | 5 |
是 | 每轮迭代第一阶段的最大循环次数 |
min_modularity_increase |
Float | [0,1] | 0.01 |
是 | 将点分配到另一社区的最小模块度增益(ΔQ) |
edge_schema_property |
[]"<@schema.?><property>" |
/ | / | 是 | 作为权重的数值类型边属性,权重值为所有指定属性值的总和;不包含指定属性的边将被忽略 |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点 |
limit |
Integer | ≥-1 | -1 |
是 | 限制返回的结果数;-1返回所有结果 |
order |
String | asc, desc |
/ | 是 | 根据count值对结果排序;该选项仅在流式返回模式下mode为2时生效 |
文件回写
该算法可生成三个文件:
配置项 |
内容 |
|---|---|
filename_community_id |
|
filename_ids |
|
filename_num |
|
CALL algo.louvain.write("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}, {
file: {
filename_community_id: "f1",
filename_ids: "f2",
filename_num: "f3"
}
})
algo(louvain).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}).write({
file: {
filename_community_id: "f1",
filename_ids: "f2",
filename_num: "f3"
}
})
结果:
_id,community_id
I,5
G,7
J,5
D,13
N,11
F,5
H,5
B,7
L,11
A,13
E,13
K,11
M,11
C,13
community_id,_ids
13,D;A;E;C;
5,I;J;F;H;
7,G;B;
11,N;L;K;M;
community_id,count
13,4
5,4
7,2
11,4
数据库回写
将结果中的community_id值写入指定点属性。该属性类型为uint32。
CALL algo.louvain.write("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}, {
db: {
property: "communityID"
}
})
algo(louvain).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}).write({
db: {
property: 'communityID'
}
})
统计回写
CALL algo.louvain.write("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}, {
stats: {}
})
algo(louvain).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}).write({
stats: {}
})
结果:
| community_count | modularity |
|---|---|
| 4 | 0.464280 |
完整返回
CALL algo.louvain.run("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1
}) YIELD r
RETURN r
exec{
algo(louvain).params({
return_id_uuid: "id",
phase1_loop_num: 5,
min_modularity_increase: 0.1
}) as r
return r
} on my_hdc_graph
结果:
| _id | community_id |
|---|---|
| I | 5 |
| G | 7 |
| J | 5 |
| D | 9 |
| N | 11 |
| F | 5 |
| H | 5 |
| B | 7 |
| L | 11 |
| A | 9 |
| E | 9 |
| K | 11 |
| M | 11 |
| C | 9 |
流式返回
流式返回支持两种模式:
| 项目 | 配置项 | 列名 |
|---|---|---|
mode |
1(默认) |
|
2 |
|
CALL algo.louvain.stream("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 6,
min_modularity_increase: 0.1
}) YIELD r
RETURN r
exec{
algo(louvain).params({
return_id_uuid: "id",
phase1_loop_num: 6,
min_modularity_increase: 0.1
}).stream() as r
return r
} on my_hdc_graph
结果:
| _id | community_id |
|---|---|
| I | 5 |
| G | 7 |
| J | 5 |
| D | 9 |
| N | 11 |
| F | 5 |
| H | 5 |
| B | 7 |
| L | 11 |
| A | 9 |
| E | 9 |
| K | 11 |
| M | 11 |
| C | 9 |
CALL algo.louvain.stream("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 6,
min_modularity_increase: 0.1,
order: "asc"
}, {
mode: 2
}) YIELD r
RETURN r
exec{
algo(louvain).params({
return_id_uuid: "id",
phase1_loop_num: 6,
min_modularity_increase: 0.1,
order: "asc"
}).stream({
mode: 2
}) as r
return r
} on my_hdc_graph
结果:
| community_id | count |
|---|---|
| 7 | 2 |
| 5 | 4 |
| 9 | 4 |
| 11 | 4 |
统计返回
CALL algo.louvain.stats("my_hdc_graph", {
return_id_uuid: "id",
phase1_loop_num: 6,
min_modularity_increase: 0.1
}) YIELD s
RETURN s
exec{
algo(louvain).params({
return_id_uuid: "id",
phase1_loop_num: 6,
min_modularity_increase: 0.1
}).stats() as s
return s
} on my_hdc_graph
结果:
| community_count | modularity |
|---|---|
| 4 | 0.397778 |
算法效率
Louvain算法通过优化的贪心算法实现了比之前的社区检测算法更低的时间复杂度,通常认为是O(N*logN),其中N是图中节点的数量,其结果也更直观。例如,在一个包含1万个节点的图中,Louvain算法的复杂度大约是O(40000);在一个包含1亿节点的连通图中,算法的复杂度大约是O(800000000)。
然而,仔细观察算法的过程,我们会发现,Louvain算法的复杂度不仅取决于节点的数量,还取决于边的数量。粗略地说,可以近似为O(N * E/N) = O(E),其中E是图中边的数量。这是因为Louvain算法的主要逻辑是计算连接到每个节点的边的权重。
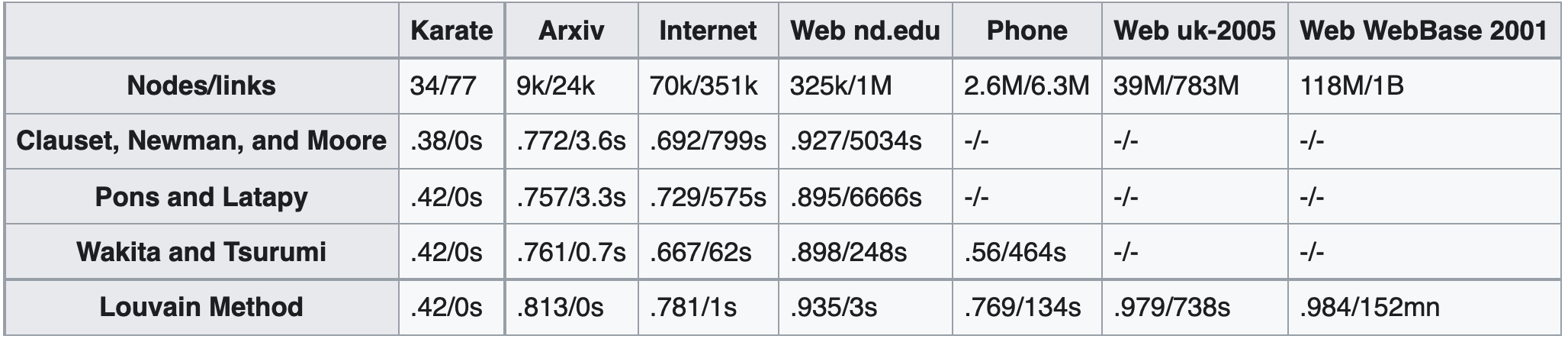
下表显示了Clauset, Newman and Moore、Pons and Latapy、Wakita and Tsurumi以及Louvain这几个社区检测算法在不同大小的图上的性能差异。对于每个算法/网络,它给出了获得的模块度和计算时间,空记录表示计算时间超过了24小时。可以清楚地看到,Louvain算法在模块度和效率方面取得了显著的(指数级)提升。
系统架构和编程语言的选择对Louvain算法的效率和最终结果都会产生影响。例如,用Python串行实现的Louvain算法可能需要数小时来处理约1万个节点的小图。此外,所使用的数据结构也会影响性能,因为该算法会频繁计算节点度和边的权重。
原生Louvain算法采用C++,但是它是串行实现的。通过尽可能多地使用并行计算,可以减少时间消耗,从而提高算法的效率。
对于中等规模包含数千万个节点和边的图集,嬴图的Louvain算法可以实时完成。对于包含超过1亿个节点和边的大图,可以在几秒钟到几分钟内完成。此外,Louvain算法的效率还受到其他因素的影响,例如数据是否写回到数据库属性或磁盘文件。这些操作会影响算法的整体计算时间。

这是Louvain算法在包含500万个节点和1亿条边的图上运行的模块性和执行时间记录。计算过程大约需要1分钟,而其他额外的操作,比如写回到数据库或生成磁盘文件,会增加约1分钟的执行时间。
