概述
优先连接(Preferential Attachment)描述的是复杂网络中常见的“强者更强”现象,即拥有更多连接的节点更有可能建立新的连接。当两个节点都拥有大量的连接时,它们形成连接的概率显著增加。这一现象在2002年被A. Barabási和R. Albert用于他们提出的BA模型,该模型用于生成随机的无标度网络:
- R. Albert, A. Barabási, Statistical mechanics of complex networks (2001)
优先连接算法通过计算每个节点的邻居数的乘积来衡量两个节点之间的相似性。它的计算公式如下:
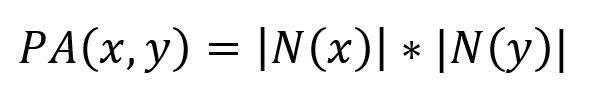
其中,N(x)和N(y)分别是与节点x和节点y相连的节点集合。
优先连接分值较高表示节点间的相似度较大,分值为0则表示两个节点间没有相似性。
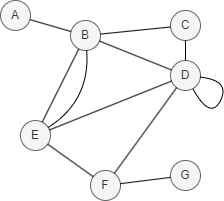
在上图中,PA(D,E) = |N(D)| * |N(E)| = |{B, C, E, F}| * |{B, D, F}| = 4 * 3 = 12。
特殊说明
- 优先连接算法忽略边的方向,按照无向边进行计算。
示例图
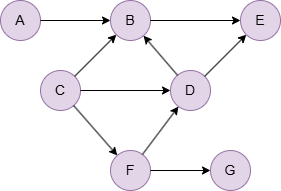
在一个空图中运行以下语句定义图结构并插入数据:
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(A)-[:default]->(B),
(B)-[:default]->(E),
(C)-[:default]->(B),
(C)-[:default]->(D),
(C)-[:default]->(F),
(D)-[:default]->(B),
(D)-[:default]->(E),
(F)-[:default]->(D),
(F)-[:default]->(G);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}]);
insert().into(@default).edges([{_from:"A", _to:"B"}, {_from:"B", _to:"E"}, {_from:"C", _to:"B"}, {_from:"C", _to:"D"}, {_from:"C", _to:"F"}, {_from:"D", _to:"B"}, {_from:"D", _to:"E"}, {_from:"F", _to:"D"}, {_from:"F", _to:"G"}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:topological_link_prediction
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
ids |
[]_id |
/ | / | 否 | 通过_id指定参与计算的第一组点;若未设置则计算所有点 |
uuids |
[]_uuid |
/ | / | 否 | 通过_uuid指定参与计算的第一组点;若未设置则计算所有点 |
ids2 |
[]_id |
/ | / | 否 | 通过_id指定参与计算的第二组点;若未设置则计算所有点 |
uuids2 |
[]_uuid |
/ | / | 否 | 通过_uuid指定参与计算的第二组点;若未设置则计算所有点 |
type |
String | Preferential_Attachment |
Adamic_Adar |
否 | 指定待计算的相似度类型;计算优先连接时,设置为Preferential_Attachment |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点 |
limit |
Integer | ≥-1 | -1 |
是 | 限制返回的结果数;-1返回所有结果 |
文件回写
CALL algo.topological_link_prediction.write("my_hdc_graph", {
ids: ["C"],
ids2: ["A","E","G"],
type: "Preferential_Attachment",
return_id_uuid: "id"
}, {
file: {
filename: "pa"
}
})
algo(topological_link_prediction).params({
projection: "my_hdc_graph",
ids: ["C"],
ids2: ["A","E","G"],
type: "Preferential_Attachment",
return_id_uuid: "id"
}).write({
file: {
filename: "pa"
}
})
结果:
_id1,_id2,result
C,A,3
C,E,6
C,G,3
完整返回
CALL algo.topological_link_prediction.run("my_hdc_graph", {
ids: ["C"],
ids2: ["A","C","E","G"],
type: "Preferential_Attachment",
return_id_uuid: "id"
}) YIELD pa
RETURN pa
exec{
algo(topological_link_prediction).params({
ids: ["C"],
ids2: ["A","C","E","G"],
type: "Preferential_Attachment",
return_id_uuid: "id"
}) as pa
return pa
} on my_hdc_graph
结果:
| _id1 | _id2 | result |
|---|---|---|
| C | A | 3 |
| C | E | 6 |
| C | G | 3 |
流式返回
CALL algo.topological_link_prediction.stream("my_hdc_graph", {
ids: ["C"],
ids2: ["A", "B", "D", "E", "F", "G"],
type: "Preferential_Attachment",
return_id_uuid: "id"
}) YIELD pa
FILTER pa.result >= 6
RETURN pa
exec{
algo(topological_link_prediction).params({
ids: ["C"],
ids2: ["A", "B", "D", "E", "F", "G"],
type: "Preferential_Attachment",
return_id_uuid: "id"
}).stream() as pa
where pa.result >= 6
return pa
} on my_hdc_graph
结果:
| _id1 | _id2 | result |
|---|---|---|
| C | B | 12 |
| C | D | 12 |
| C | E | 6 |
| C | F | 9 |
