概述
有向图的拓扑排序(Topological Sort)是指将图中的节点按照一定的顺序进行排列,使得每条边的起点在终点之前。需要注意的是,拓扑排序仅适用于有向无环图(DAG)。
拓扑排序在计算机科学和其他领域有着各种应用。在项目管理和作业调度中,拓扑排序能够根据任务之间的依赖关系确定任务执行的最佳顺序。它还可用于解决软件开发中模块、库或组件之间的依赖关系。这一算法可以按照正确的顺序解决依赖关系,减少冲突和潜在错误的发生。
基本概念
有向无环图(DAG)
有向无环图(Directed Acyclic Graph, DAG)是指不存在有向环路(Cycle)的有向图。换句话说,在DAG中无法从任意一个节点v出发,经过一条有向路径后又回到节点v。
如下所示,第一个和第二个图是DAG,而第三个图中包含一个有向循环(B→C→D→B),不符合DAG的定义。
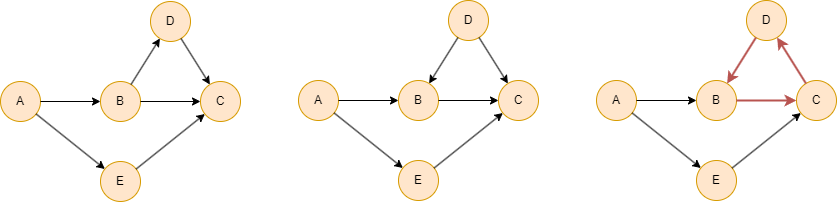
是否可以进行拓扑排序常作为判断一个有向图是否为DAG的标准。
拓扑排序
每个DAG至少有一种拓扑排序。
在上述示例中,第一个图中的节点有3种可能的排序:
- A, E, B, D, C
- A, B, E, D, C
- A, B, D, E, C
当DAG中存在包含所有节点的有向路径时,DAG才具有唯一的拓扑排序,此时排序与路径中节点出现的顺序相同。
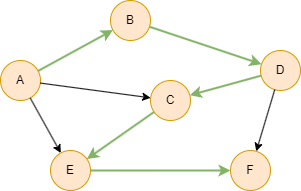
在下面的示例中,图中的节点只有1种可能的排序:A, B, D, C, E, F。
特殊说明
在存在环路的图上运行拓扑排序算法将导致一些节点在排序中被忽略掉,被忽略的节点包括:
- 环路(包括自环)中的节点;
- 环路中的节点通过出边能触达的其他节点。
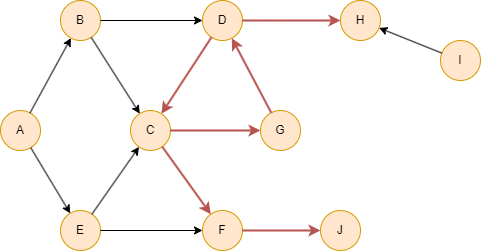
在以下的示例中,首先忽略环路中的节点C、D和G,其次忽略从环路节点出边可达的其他节点,包括节点F、J和H。下图拓扑排序结果为:A, I, B, E。
如果一个图是非连通的,或是因为忽略上述构成环路和受环路影响的节点后变成非连通,拓扑排序会分别在每个连通分量内进行,并统一返回排序结果。孤点也不会被忽略。
示例图
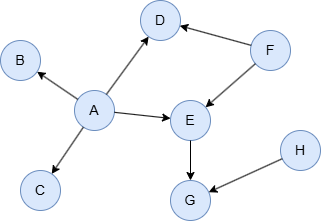
在一个空图中运行以下语句定义图结构并插入数据:
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(H:default {_id: "H"}),
(A)-[:default]->(B),
(A)-[:default]->(C),
(A)-[:default]->(D),
(A)-[:default]->(E),
(E)-[:default]->(G),
(F)-[:default]->(D),
(F)-[:default]->(E),
(H)-[:default]->(G);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}, {_id:"H"}]);
insert().into(@default).edges([{_from:"A", _to:"B"}, {_from:"A", _to:"C"}, {_from:"A", _to:"D"}, {_from:"A", _to:"E"}, {_from:"E", _to:"G"}, {_from:"F", _to:"D"}, {_from:"F", _to:"E"}, {_from:"H", _to:"G"}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:topological_sort
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点;该选项仅在文件回写模式下生效 |
文件回写
CALL algo.topological_sort.write("my_hdc_graph", {
return_id_uuid: "id"
}, {
file: {
filename: "sort"
}
})
algo(topological_sort).params({
projection: "my_hdc_graph",
return_id_uuid: "id"
}).write({
file: {
filename: "sort"
}
})
结果:
_id
F
H
A
B
C
D
E
G
完整返回
CALL algo.topological_sort.run("my_hdc_graph", {}) YIELD r
RETURN r
exec{
algo(topological_sort).params() as result
return result
} on my_hdc_graph
[{"id":"F","uuid":"2882304861028745219","schema":"default","values":{}}]
[{"id":"H","uuid":"3386708019294240772","schema":"default","values":{}}]
[{"id":"A","uuid":"10016006670783610881","schema":"default","values":{}}]
[{"id":"B","uuid":"3530823207370096641","schema":"default","values":{}}]
[{"id":"C","uuid":"12033619303845593090","schema":"default","values":{}}]
[{"id":"D","uuid":"288231475663339522","schema":"default","values":{}}]
[{"id":"E","uuid":"10520409829049106435","schema":"default","values":{}}]
[{"id":"G","uuid":"13690943966717935617","schema":"default","values":{}}]
流式返回
CALL algo.topological_sort.stream("my_hdc_graph", {}) YIELD r
FOR node IN r
RETURN node._id
exec{
algo(topological_sort).params({}).stream() as r
uncollect r as node
return node._id
} on my_hdc_graph
结果:
| node._id |
|---|
| F |
| H |
| A |
| B |
| C |
| D |
| E |
| G |
