概述
单源最短路径问题(Single-Source Shortest Path, SSSP)计算的是从图中一个源节点到其余所有可达节点的最短路径。最短路径是指全部可能的路径中,所有边的权重和最小的路径;在无权图的情况下,是指边的数量最少的路径。最短路径的成本(或距离)是指所有边的权重和或数量。
Delta-Stepping(增量步进)单源最短路径算法可以看成是 Dijkstra算法的一种变体,具有并行计算的潜力。
算法的相关资料如下:
- U. Meyer, P. Sanders, Δ-Stepping: A Parallel Single Source Shortest Path Algorithm (1998)
基本概念
Delta-Stepping单源最短路径
Delta-Stepping单源最短路径算法引入了“桶”(Bucket)的概念,并且以一种更粗粒度的方式执行松弛操作。该算法利用一个增量参数delta (Δ) > 0来实现以下目标:
- 维护一个数组B,其中B[i]包含距离在范围[iΔ, (i+1)Δ)内的节点。因此,Δ也被称为“步长”或“桶宽”。
- 区分图中权重≤Δ的“轻边”(Light Edges)和权重>Δ的“重边”(Heavy Edges)。在松弛过程中,优先考虑轻边节点,因为它们的权重更低,更有可能产生较短的路径。
松弛操作是指通过考虑经过节点u的路径,更新与节点u相连的节点v的距离,使其获得可能的更短距离。具体来说,节点v的距离会被更新为dist(v) = dist(u) + w(u,v),其中w(u,v)是边(u,v)的权重。此更新仅在当前dist(v)大于dist(u) + w(u,v)时进行。
在Delta-Stepping单源最短路径算法中,松弛操作还包括根据更新后的距离值将被松弛的节点分配到相应的桶中。
我们将通过计算示例图中以b为源节点的无向加权最短路径来解释Delta-Stepping单源最短路径算法的基本实现,设置Δ为3:
1. 算法开始时,所有节点的距离都被设为无穷大,除了源节点,它的距离被设为0。将源节点分配到桶B[0]。
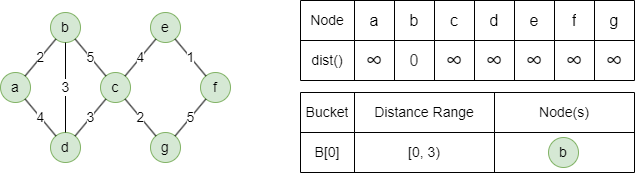
2. 在每次迭代中,从第一个非空桶B[i]中移除所有节点:
- 松弛所有被移除节点的轻边邻居,被松弛的节点可能被分配到B[i]或B[i+1]桶;推迟对重边邻居的松弛。
- 如果B[i]中又有节点加入,重复上述操作直到B[i]为空。
- 松弛所有推迟的重边邻居。

松弛轻边邻居a为dist(a) = min(0+2,∞) = 2,d为dist(b) = min(0+3,∞) = 3

轻边邻居b无法被松弛
松弛重边邻居c为 dist(c) = min(0+5,∞) = 5,d无法被松弛
3. 重复第2步,直到所有桶为空。
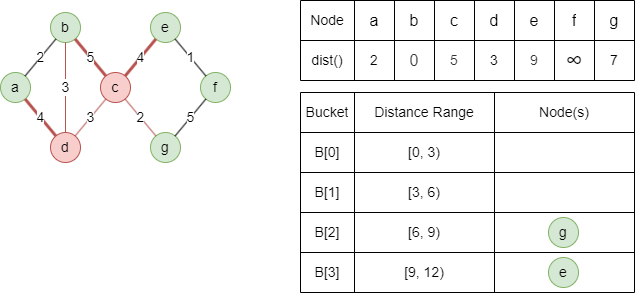
松弛轻边邻居g为dist(g) = min(5+2,∞) = 7,b、c和d无法被松弛
松弛重边邻居e为dist(e) = min(5+4,∞) = 9,a和b无法被松弛
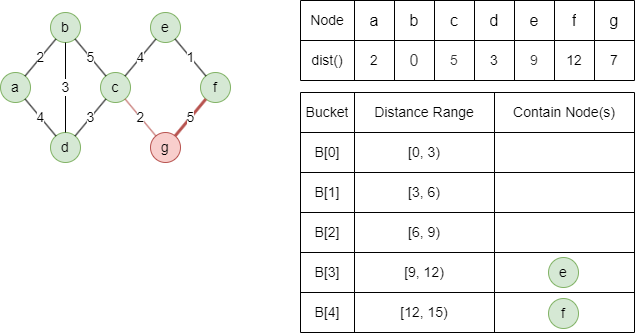
轻边邻居c无法被松弛
松弛重边邻居f为dist(f) = min(7+5,∞) = 12
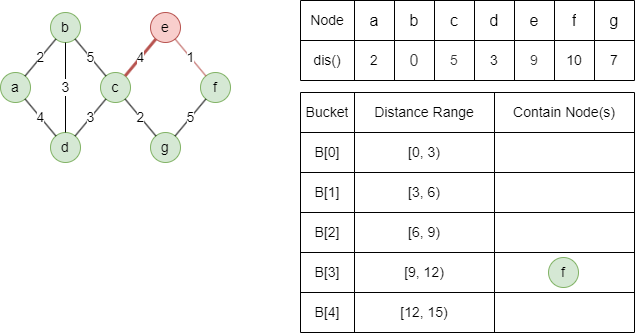
松弛轻边邻居f为dist(f) = min(9+1,12) = 10
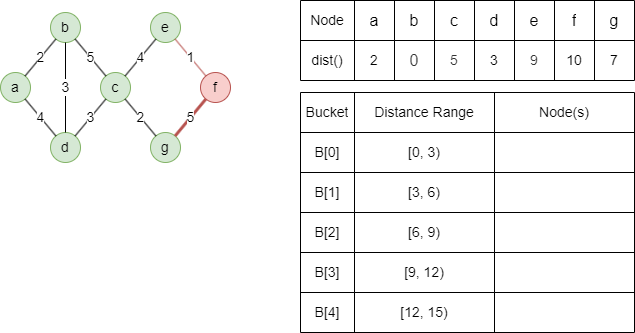
轻边邻居e无法被松弛
重边邻居g无法被松弛
所有桶为空,算法结束
通过将节点放入不同的桶进行并行处理,Delta-Stepping算法可以更有效地利用可用的计算资源,适用于大规模图和并行计算环境。
特殊说明
- Delta-Stepping单源最短路径算法适用于具有非负边权重的图。如果存在负权重,Delta-Stepping单源最短路径算法输出的结果也许是不正确的。这种情况建议使用SPFA算法。
- 如果两个节点之间存在多条最短路径,算法会找出所有这些路径。
- 在非连通图中,算法只输出源节点所在的连通分量内所有节点到源节点的最短距离。
示例图
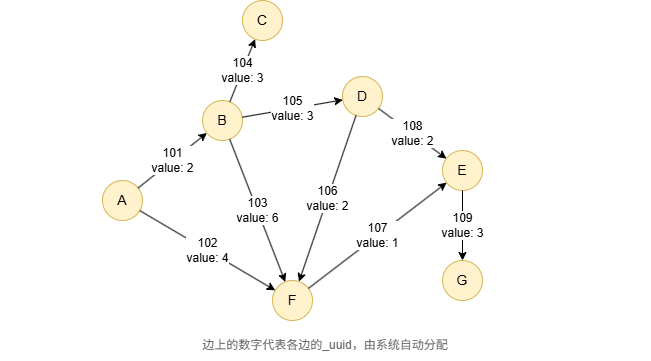
在一个空图中运行以下语句定义图结构并插入数据:
ALTER EDGE default ADD PROPERTY {
value int32
};
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(A)-[:default {value: 2}]->(B),
(A)-[:default {value: 4}]->(F),
(B)-[:default {value: 3}]->(C),
(B)-[:default {value: 3}]->(D),
(B)-[:default {value: 6}]->(F),
(D)-[:default {value: 2}]->(E),
(D)-[:default {value: 2}]->(F),
(E)-[:default {value: 3}]->(G),
(F)-[:default {value: 1}]->(E);
create().edge_property(@default, "value", int32);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}]);
insert().into(@default).edges([{_from:"A", _to:"B", value:2}, {_from:"A", _to:"F", value:4}, {_from:"B", _to:"F", value:6}, {_from:"B", _to:"C", value:3}, {_from:"B", _to:"D", value:3}, {_from:"D", _to:"F", value:2}, {_from:"F", _to:"E", value:1}, {_from:"D", _to:"E", value:2}, {_from:"E", _to:"G", value:3}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:sssp
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
ids |
_id |
/ | / | 否 | 通过_id指定单个源节点 |
uuids |
_uuid |
/ | / | 否 | 通过_uuid指定单个源节点 |
direction |
String | in, out |
/ | 是 | 指定最短路径中所有边的方向,in表示仅包含入边,out表示仅包含出边;若未设置则不考虑边方向 |
edge_schema_property |
[]"<@schema.?><property>" |
/ | / | 是 | 作为权重的数值类型边属性,权重值为所有指定属性值的总和;不包含指定属性的边将被忽略 |
record_path |
Integer | 0, 1 |
0 |
是 | 是否在结果中包含最短路径。设定为1时,返回totalCost和最短路径;设置为0时,仅返回totalCost |
impl_type |
String | delta_stepping |
beta |
否 | 指定SSSP算法的执行类型;计算Delta-Stepping单源最短路径时,设置为delta_stepping;beta是嬴图默认最短路径算法 |
delta |
Float | >0 | 2 |
是 | 增量delta的值;仅在impl_type设置为delta_stepping时生效 |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点。仅可使用_uuid表示边 |
limit |
Integer | ≥-1 | -1 |
是 | 限制返回的结果数;-1返回所有结果 |
order |
String | asc, desc |
/ | 是 | 根据totalCost值对结果排序 |
文件回写
CALL algo.sssp.write("my_hdc_graph", {
ids: "A",
edge_schema_property: "@default.value",
impl_type: "delta_stepping",
return_id_uuid: "id"
}, {
file: {
filename: "costs"
}
})
algo(sssp).params({
projection: "my_hdc_graph",
ids: "A",
edge_schema_property: "@default.value",
impl_type: "delta_stepping",
return_id_uuid: "id"
}).write({
file: {
filename: "costs"
}
})
结果:
_id,totalCost
G,8
D,5
F,4
B,2
E,5
C,5
CALL algo.sssp.write("my_hdc_graph", {
ids: "A",
edge_schema_property: '@default.value',
impl_type: 'delta_stepping',
delta: 2,
record_path: 1,
return_id_uuid: "id"
}, {
file: {
filename: "paths"
}
})
algo(sssp).params({
projection: "my_hdc_graph",
ids: "A",
edge_schema_property: '@default.value',
impl_type: 'delta_stepping',
delta: 2,
record_path: 1,
return_id_uuid: "id"
}).write({
file: {
filename: "paths"
}
})
结果:
totalCost,_ids
8,A--[102]--F--[107]--E--[109]--G
5,A--[101]--B--[105]--D
5,A--[102]--F--[107]--E
5,A--[103]--B--[104]--C
4,A--[102]--F
2,A--[101]--B
完整返回
CALL algo.sssp.run("my_hdc_graph", {
ids: 'A',
edge_schema_property: 'value',
impl_type: 'delta_stepping',
delta: 3,
record_path: 0,
return_id_uuid: 'id',
order: 'desc'
}) YIELD r
RETURN r
exec{
algo(sssp).params({
ids: 'A',
edge_schema_property: 'value',
impl_type: 'delta_stepping',
delta: 3,
record_path: 0,
return_id_uuid: 'id',
order: 'desc'
}) as r
return r
} on my_hdc_graph
结果:
| _id | totalCost |
|---|---|
| G | 8 |
| D | 5 |
| E | 5 |
| C | 5 |
| F | 4 |
| B | 2 |
流式返回
CALL algo.sssp.stream("my_hdc_graph", {
ids: 'A',
edge_schema_property: '@default.value',
impl_type: 'delta_stepping',
record_path: 1,
return_id_uuid: 'id'
}) YIELD r
RETURN r
exec{
algo(sssp).params({
ids: 'A',
edge_schema_property: '@default.value',
impl_type: 'delta_stepping',
record_path: 1,
return_id_uuid: 'id'
}).stream() as r
return r
} on my_hdc_graph
结果:
totalCost |
_ids |
|---|---|
| 8 | ["A","102","F","107","E","109","G"] |
| 5 | ["A","101","B","105","D"] |
| 5 | ["A","102","F","107","E"] |
| 5 | ["A","101","B","104","C"] |
| 4 | ["A","102","F"] |
| 2 | ["A","101","B"] |
