概述
特征向量中心性(Eigenvector Centrality)算法度量的是节点影响的传递。来自高分值节点的关系对节点分值贡献大于来自低分值节点的关系,节点有高分值意味着它连接到许多高分值节点。特征向量中心性强调节点所处的周围环境,例如在疾病传播中,特征向量中心性较大的节点距离传染源更近的可能性更大,需要格外防范。
Google 著名的 PageRank 算法是特征向量中心性算法的一个变种,用来进行网页排名。
特征向量中心性的取值范围是 [0,1],数值越大中心性越大。
基本概念
特征值和特征向量
特征值和特征向量是矩阵理论的重要概念之一。A 为 n 阶矩阵,若常数 λ 和 n 维非 0 向量 x 满足 Ax = λx,那么称数 λ 为 A 的特征值(Eigenvalue), x 为 A 的对应于特征值 λ 的特征向量(Eigenvector)。
n 阶矩阵的特征值可通过特征方程 |A - λE| = 0 求解,其中 E 为 n 阶单位矩阵,特征方程的 n 个根(可能有重根)即为 n 个特征值 λ1、λ2、... 、λn。对于每个特征值,相应的特征向量可以通过求解特征方程 (A – λE)x = 0 得到,特征向量可以有无穷个。在这些特征值中,绝对值最大的特征值称为主特征值,主特征值对应的特征向量即为主特征向量,它包含矩阵最多的信息。

上面的例子中,矩阵 A 的特征值有 5 个,与绝对值最大的特征值 λ1 对应的特征向量 x1 就是主特征向量。
特征向量中心性
图上节点间通过边互相影响的关系可以用矩阵表示,矩阵的特征向量所度量的节点中心性,就是特征向量中心性。
幂迭代法
求解矩阵特征值和特征向量的常用方法是特征多项式计算法,但在实践中,该计算相当耗费资源且无法计算大型矩阵。Ultipa 的特征向量中心性算法使用幂迭代法求解矩阵的主特征向量,此方法在保证精度的同时也极大提高计算效率。
幂迭代法的计算过程很简单。对于 n 阶矩阵 A,任意选取一个 n 维初始向量 v(0),并按照以下规律进行迭代,继续构造向量:
- v(1) = Av(0)
- v(2) = Av(1) = A2v(0)
- ...
- v(k) = Av(k-1) = Akv(0)
当 k 足够大时,v(k) 即可视为 A 的特征向量。幂迭代法的收敛性理论上是可以推导证明的,在此不赘述。
此方法存在的问题是,v(k) 中的非 0 元素值会随着 k 的增大而大幅增大,为避免计算过程中数据溢出,每步迭代时,算法对 v(k) 中每个元素的绝对值进行 L2 范数归一化处理。
Ultipa 的特征向量中心性算法规定迭代的收敛偏差 tolerance 为归一化后的向量 v(k) 所有元素绝对值的和的变化,当该变化值小于规定的收敛偏差时,迭代结束,若迭代轮数达到限制,迭代也会结束。
特殊处理
孤点、不连通图
由于没有连接其他节点的边,孤点的特征向量中心性完全取决于其自环边。
自环边
自环边的权重值只会被计算一次。
有向边
对于每个节点,特征向量中心性算法只考虑其入边,即接收到的来自邻居节点的影响。入边为 0 的节点的特征向量中心性分值无限趋近于 0。
结果和统计值
以下面包含 7 个节点的网页间链接关系图为例,所有边的权重为 1,运行特征向量中心性算法,最多迭代 20 次,收敛偏差为 0.01:
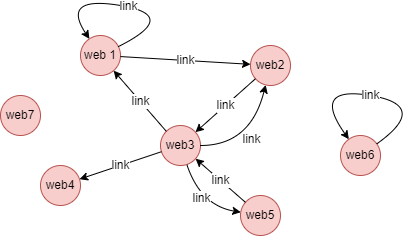
算法结果:为每个点计算特征向量中心性,根据算法执行方式,返回 _id、rank 两列或 _uuid、rank 两列
| _uuid | _id | rank |
|---|---|---|
| 1 | web1 | 0.57355899 |
| 2 | web2 | 0.57355601 |
| 3 | web3 | 0.45988801 |
| 5 | web5 | 0.25517300 |
| 4 | web4 | 0.25516701 |
| 6 | web6 | 0.018536000 |
| 7 | web7 | 0.0000060000002 |
算法统计值:无
命令及配置项
- 命令:
algo(eigenvector_centrality) params()参数配置项如下:
| 名称 | 类型 | 默认值 |
规范 |
描述 |
|---|---|---|---|---|
| max_loop_num | int | 20 | >=1 | 算法最大迭代轮数 |
| tolerance | float | 0.001 | (0,1) | 收敛偏差,即归一化后的向量所有元素绝对值的和的变化,若变化值小于收敛偏差,则算法结束 |
| edge_weight_property | @<schema>?.<property> |
/ | 数值类的边属性,需LTE | 边权重所在的一个或多个属性名称,带不带 schema 均可,无该属性的边不参与计算;忽略表示不加权 |
| limit | int | -1 | >=-1 | 需要返回的结果条数,-1 或忽略表示返回所有结果 |
| order | string | / | ASC/DESC,大小写不敏感 | 对返回结果进行排序;忽略表示不排序 |
示例:计算所有点的特征向量中心性,最多迭代 20 次,收敛偏差为 0.01
algo(eigenvector_centrality).params({
max_loop_num: 20,
tolerance: 0.01
}) as centrality
return centrality
算法执行
任务回写
1. 文件回写
| 配置项 | 各列数据 |
|---|---|
| filename | _id,rank |
示例:计算所有点的特征向量中心性,最多迭代 20 次,收敛偏差为 0.01,将算法结果回写至名为 rank 的文件
algo(eigenvector_centrality).params({
max_loop_num: 20,
tolerance: 0.01
}).write({
file: {
filename: "rank"
}
})
2. 属性回写
| 配置项 | 回写内容 | 类型 | 数据类型 |
|---|---|---|---|
| property | rank |
点属性 | float |
示例:计算所有点的特征向量中心性,最多迭代 20 次,收敛偏差为 0.01,将算法结果回写至名为 ec 的点属性
algo(eigenvector_centrality).params({
max_loop_num: 20,
tolerance: 0.01
}).write({
db: {
property: "ec"
}
})
3. 统计回写
算法无统计值。
直接返回
| 别名序号 | 类型 | 描述 | 列名 |
|---|---|---|---|
| 0 | []perNode | 点及其特征向量中心性 | _uuid, rank |
示例:计算所有点的特征向量中心性,最多迭代 20 次,收敛偏差为 0.01,边权重位于 @link.score 属性上,将算法结果定义为别名 ec 并返回
algo(eigenvector_centrality).params({
max_loop_num: 20,
tolerance: 0.01,
edge_weight_propery: @link.score
}) as ec
return ec
流式返回
| 别名序号 | 类型 | 描述 | 列名 |
|---|---|---|---|
| 0 | []perNode | 点及其特征向量中心性 | _uuid, rank |
示例:计算所有点的特征向量中心性,最多迭代 20 次,收敛偏差为 0.01,分别统计分值大于 0.5 和小于等于 0.5 的节点数量
algo(eigenvector_centrality).params({
max_loop_num: 20,
tolerance: 0.01
}).stream() as results
WITH CASE
when results.rank > 0.5 then "attention"
when results.rank <= 0.5 then "normal"
END as cat
group by cat
return table(cat, count(cat))
实时统计
算法无统计值。
