本文介绍图数据的基本构成，以及如何使用 UQL 描述和表达图数据，这些概念是学习和掌握 Ultipa 产品的前提。
图数据
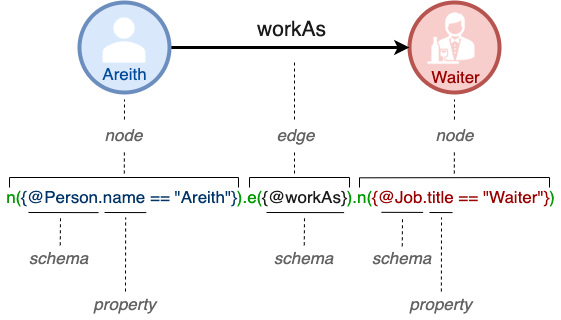
点
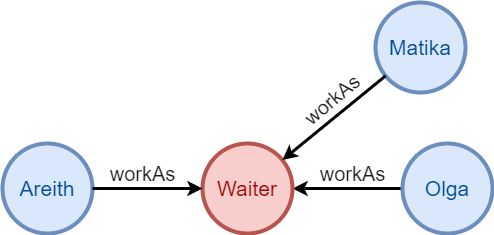
图1 中用圆圈表示的 Areith 和 Waiter 是点。
点表示真实世界中的实体。
边
图1 中的箭头 workAs 是一条边，由 Areith 指向 Waiter。
边表示实体之间的关系。
Schema
图1 中代码里出现的 Person，Job 和 workAs 是 schema，可理解为模式。
Schema 表示点、边的不同类型。
属性
图1 中代码里出现的 name 和 title 是属性。
属性是 schema 的组成部分，用来具体描述某种 schema 的构成。
路径
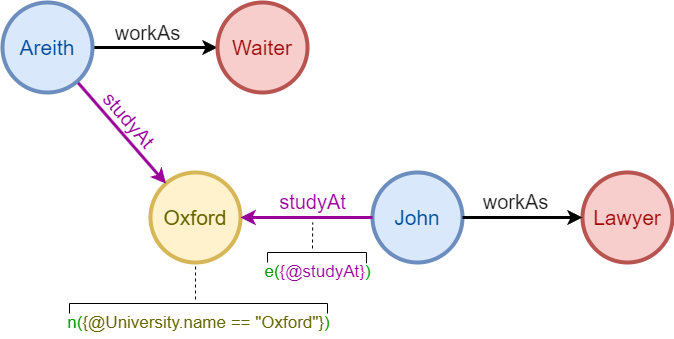
图2 中由 Areith、worksAs、Waiter 所形成的连续且点、边交替出现的序列 是一条路径。同理，由 Waiter、worksAs、Areith、studyAt、Oxford 构成的序列也是一条路径。
路径由点开始，以点结束，包含至少一条边。路径表达了实体之间的多步关联关系，也是图计算中经常查询的目标。
描述点
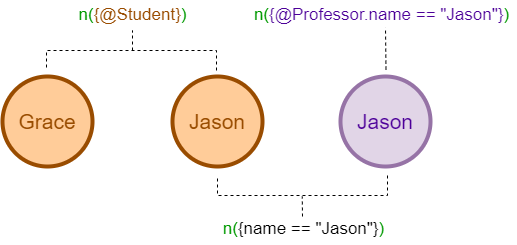
很多 UQL 参数都可以描述点，以 n() 为例：
n() // 任何点
n({@Student}) // schema 为 'Student' 的点
n({name == "Jason"}) // 属性 'name' 为 'Jason' 的点
n({@Student.name == "Jason"}) // schema 为 'Student' 且属性 'name' 为 'Jason' 的点
n(as a) // 任何一个点，并命名为 'a'
n({@Student} as a) // ...
...
以上描述的语法特征：
- 参数
n()内为空时不对点做任何要求 - 过滤点的 schema 时须用到符号
@ - 点的 schema 和属性可以分开描述，也可以联合过滤
- 给满足要求的点定义别名时须用到关键词
as
UQL 中可以用来描述点的参数有：
nodes()：用于点的查找、更新、删除n()：用于模板查询（一种路径查询方法）nf()：用于模板查询src()：用于非模板的路径查询dest()：用于非模板的路径查询node_filter()：用于非模板的路径查询
描述边
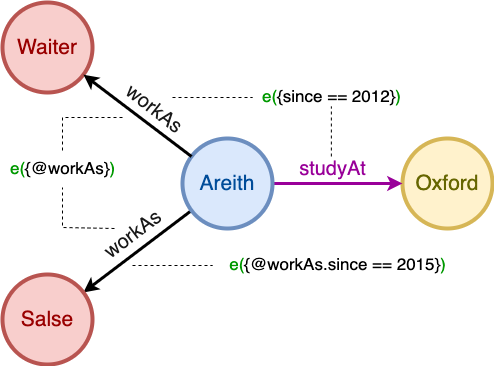
以 e() 为例说明如何对边进行描述：
e() // 任何边
e({@workAs}) // schema 为 'workAs' 的边
e({since == 2012}) // 属性 'since' 为 '2012' 的边
e({@workAs.since == 2012}) // schema 为 'workAs' 且属性 'since' 为 '2012' 的边
e(as b) // 任何一个边，并命名为 'b'
e({@workAs} as b) // ...
...
与 n() 类似，使用参数 e() 对边进行描述时有以下特征：
- 参数
e()内为空时不对边做任何要求 - 过滤边的 schema 时须用到符号
@ - 边的 schema 和属性可以分开描述，也可以联合过滤
- 给满足要求的边定义别名时须用到关键词
as（注意：有时e()中不支持定义别名）
UQL 中可以用来描述边的参数有：
edges()：用于边的查找、更新、删除e()：用于模板查询le()：用于模板查询re()：用于模板查询edge_filter()：用于非模板的路径查询
描述路径（模板）
使用 n() 和 e() 描述的路径称为模板：
// 任何一步路径
n().e().n()
// 任何二步路径
n().e().n().e().n()
n().e()[2].n()
// 表示 'Person-workAs-waiter' 的一步路径
// 将其中表示 Person 的点命名为 'individual'，将这些路径命名为 'career'
n({@Person} as individual).e({@workAs}).n({@Job.title == "Waiter"}) as career
// 表示 'Areith-workAs-Job-workAs-Person' 的二步路径
// 将其中表示 Job 的点命名为 'job'，将末尾的 Person 命名为 'other'
n({@Person.name == "Areith"}).e({@workAs}).n({@Job} as job).e({@workAs}).n({@Person} as other)
...
路径模板的特征：
- 是一种非常直观、形象的路径描述方式
- 路径中的某个点、某个边、整条路径都可以定义别名
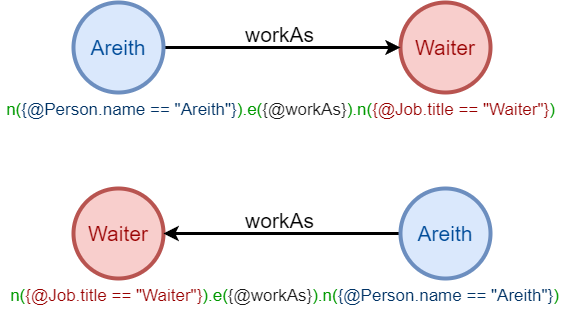
图6 中两个模板所描述的路径是否相同？由于 Ultipa 的路径是从左向右书写并解析的，这两个路径模板的点、边顺序不一致，因此不相同。但它们都描述了相同的图数据。